본 글은 학교 '머신러닝' 수업을 들으며 공부한 내용을, 저의 말로 바꿔서 남에게 설명해주듯이 쓰는 글입니다.
다시 한번 복습하는 과정에서 Coursera Andrew Ng 교수님의 강의를 일부 수강하였고, 인터넷 검색 등을 통해 내용을 보충하였습니다.
너무 쉬운 개념들은 따로 정리하지 않았습니다. 따라서 해당 글에는 적히지 않은 개념들이 일부 있을 수 있습니다.
본 글은 Andrew Ng 교수님의 'machine learning' 수업 강의 노트를 일부 사용하였습니다.
본 글에 사용된 강의노트 사진들 대부분의 저작권은 'DeepLearning.AI'에 귀속되어 있음을 밝히며,
본 글은 'DeepLearning.AI'의 'Copyright rights'에 따라 수익 창출을 하지 않고,
또한 해당 정책에 따라 '개인 공부 및 정보 전달'이라는 교육적 목적으로 글을 작성함을 밝힙니다.

Prioritizing what to work on(우선순위 정하기): Spam classification example(스팸 분류기 예제)
스팸메일인지 아닌지 구분하는 학습 알고리즘을 지도 학습으로 구현한다고 해 보자.
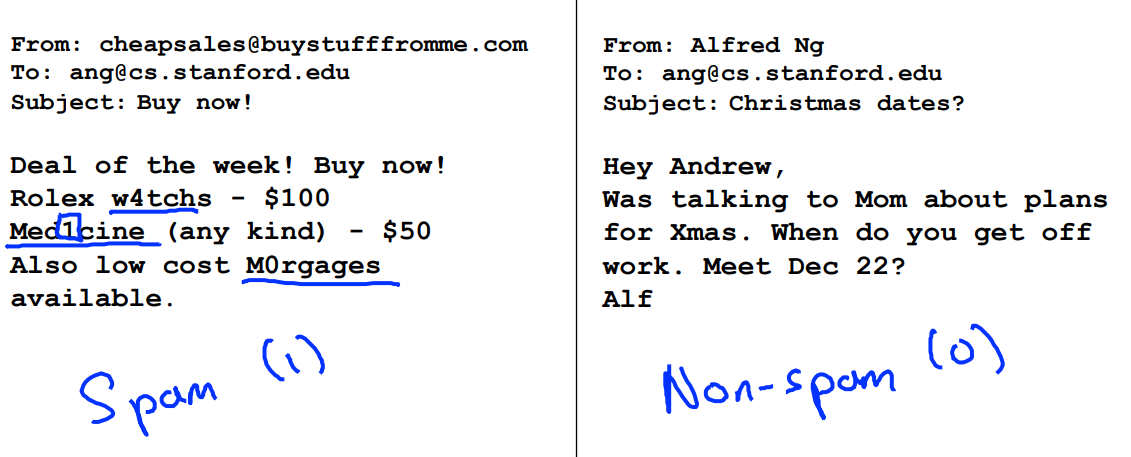
위 사진의 왼쪽은 스팸 메일, 오른쪽은 스팸이 아닌 메일임.
내 목표는, 각각의 메일을 입력했을 때, 왼쪽은 1 (= Spam), 오른쪽은 0 (Non-Spam) 이라는 결과값을 내뱉어줄 모델을 설계하는 것임.
이 때, 입력에 사용되는 피쳐로는 '단어'를 사용해보자. 이메일이 스팸인지 아닌지 판단할 수 있을만한 단어 목록들을 사용하는 것이다. discount(할인), buy(구매)와 같은 단어들을 피쳐로 사용하여, 이러한 스팸 단어들이 어떤 게 어떻게 몇 개가 있냐에 따라 스팸이다 아니다를 분류해볼 수 있다. 이 때 각각의 피쳐들은 1(그 단어가 있음) 또는 0(그 단어가 없음)의 값을 가진다.
예를 들어 discount나 buy 같은 게 1이면 그게 스팸일 확률이 더 높아질 것이고, yeonwoo 같이 수신자의 이름같은 게 1이면(단어가 있으면) 스팸일 확률은 낮아질 것이다. (뭐 내 실제 이름 알면 스팸일 확률이 더 낮지 않겠음?)

위와 같이 100개의 피쳐를 사용하겠다 하면, 피쳐 벡터 x는 100차원이 된다.
(참고로, 실제로는 training set에서 10000~50000 사이 정도 개수만큼 단어들을 선택해 피쳐로 사용한다.)
이제, 이 스팸 분류기의 성능을 향상시키려면(=error를 줄이려면) 어떻게 하면 좋을까?
다음과 같은 선택지들이 있다.
1. 더 많은 데이터 모으기
-> 항상 도움이 되진 않음.
2. 이메일 헤더에 있는 라우팅 정보를 반영해주는 피쳐 만들기
-> 스팸 이메일 분류기는 이게 좋음. 스패머가 이메일 보낼 때 가짜 이메일 헤더를 쓰거나, 특이한 경로로 보내거나 등등 할 수 있는데 그러한 내역들이 이메일 헤더에 남음.
3. 이메일 내용의 메세지들을 더 정교하게 다뤄줄 수 있는 피쳐 만들기
ex. discount와 discounts를 같게 다룰건가? 어떡할거지?
4. (고의적인) 오타를 어떻게 처리할지에 대한 알고리즘 개발하기
ex. Morgages 뿐만 아니라 M0rgages 도 반영되도록
Error analysis
추천되는 방법은 다음과 같다.
1. 빠르게 구현할 수 있는 알고리즘부터 구현하기. 그리고 그걸 cv set으로 테스트하기.
-> 24시간 내에.
2. learning curve를 그려서 더 많은 데이터나 피쳐 등이 도움이 될 지 살펴보기.
-> 학습 곡선이 없으면 암것도 뭐 시도할 cue가 없음...
3. 에러 분석 : cv set으로 테스트했을 때 error가 많이 나오는 놈을 보셈. 걔가 어떤 유형의 이메일을 잘 못 판단하는지 직접 확인. 이를 통해 새로운 피쳐를 설계할 영감을 얻을 수 있음.
예시를 들어보자. cv set의 크기가 500이고, 알고리즘이 100개의 메일을 잘못 분류했다(error을 100개 냈다)고 해보자. 그러면
1. 어떤 유형의 메일들이 오류를 많이 발생시켰는지
2. 어떤 유형의 피쳐가 오류이냐 아니냐를 잘 구별할 수 있을지
살펴봐야 한다.

위와 같이, steal passwords을 시도하려는 이메일에 대해 53번의 error가 있었음. 이게 가장 많은 error을 유발한 유형이잖음? 그래서 이 53개의 이메일의 어떤 특징이 스팸이라고 구별할 만한지 확인해보면, 그 중 32개의 이메일이 스팸스러운 구두점을 사용했다.
따라서, 이 경우는 스팸스러운 구두점 문제를 처리해줄 수 있는 정교한 피쳐를 설계하는 게 좋을 것이다.
***여기서, 이런 오류 분석과 이를 통해 어떤 개선을 해나갈지 구상하는 건 test 단계가 아닌 cv 단계에서 해야만 한다!!!!!!
test는 최종적으로 이제 평가를 해야하는데, test껄로 새 피쳐를 설계해나가면, test set에 특화된 피쳐들을 설계하게 될 수 있다. 이렇게 되면 generalizatize가 잘 됐는지 평가가 힘들다.
여담) incremental learning라는 게 있는데, 클래스를 하나씩 증가시키는 거임. 20개 class를 old 15개, new 5개로 나눔. 처음엔 old 15개로, 그 다음부턴 new 1개, 2개, ..., 5개.
incremental learning은 새로운 class에 잘 되도록 generalized가 잘 되도록 하는 게 목표인데... 근데 실제론 모델 성능을 평가하잖음. 그러다보니 old class에만 집중하게 되는 경향이 있음.
이게 뭔 소리냐... 예를 들어, old에 개, 강아지, 고양이, 같은 게 있고, new에 아이스크림, 사과, 같은 게 있음. 이거 성능 낼 때, 총 6번 시행에 대해 각각 accuracy 20개에 대해 산술평균을 구해 산술평균을 구하지 않겠음? 그러니까 old에 있는 걸 성능개선을 많이 하면 더 성능이 좋다고 평가받으니까, old class들 성능 개선에만 집중하게 되는 거임. 아이스크림, 사과는 accuracy가 잘 안나와도 뭐 ... 냅두고...
-> 이거 잘 이해안가긴 하는데 얼추 뭔 느낌인진 알겠는듯?
Error metrics for skewed classes
여담) 만약 내가 사진 가지고 분류하려는데, 내 모델이 곰이나 사자같은건 분류를 잘 하는데, 사람의 신발이나 코같은걸 분류를 잘 못함. 그럼 내 모델이 지금 어떠고, 어떻게 개선해나가야 할까. ex. 내 모델이 지금 조그마한 물체는 인식을 잘 못하니, 조그마한 물체를 잘 인식할 수 있는 레이어를 추가해야겠다. 이런식으로 가이드를 제시해주는거임.

자, 이번엔 예시를 하나 들어보자.
로지스틱 회귀때 했던 예시이다. 나는 환자가 암인지 아닌지 그 여부를 분류하는 모델을 만들었다. y = 1이면 암, y = 0이면 암이 아닌 것이다. 그리고 내 결과 h 또한 1 또는 0이다.
이 때, 내가 만든 모델이 test set에 대해 1%의 error을 가졌다. 즉, 99%의 진단은 정확했다.
이러면 일반적으론 괜찮은 모델일 수 있다. 99% 정확도면은...
근데... 만약 data set의 0.5%, 즉 환자의 0.5%만이 암에 걸려있다면??
그래서, 만약 "무조건 암이 아니라고 예측하는, 즉 무조건 h = 1을 출력하는 모델"을 개발한다면??
위 경우 0.5%의 error을 가지게 된다. 즉, 99.5%의 진단은 정확했다. 따라서 전자 모델보다 후자 모델이 성능이 더 낫게 된다.
암 환자 사례와 같이, 이렇게 data가 어떤 class로 극단적으로 몰려있을 경우, 이를 skewed class라 한다.
여기서, 우리는 "정확도(accuracy)"라는 지표를 사용해 각 모델을 평가한 것이다. 후자의 정확도가 99.5%로 전자의 정확도 99%보다 높다. 그러면, 후자 모델을 택하는 게 나을까? 이는 정확도만으로 판단하기는 좀 위험할 수 있다. 실제론 정밀도(precision)이나 재현율(recall)와 같은 값들의 대소비교는 다를 수 있고, 그에 따라 각 모델의 장단점이 달라질 수 있기 때문이다. 우리는 이런 skewed class를 다양한 관점에서 판단하기 위해, 새 measure을 도입해야 한다.
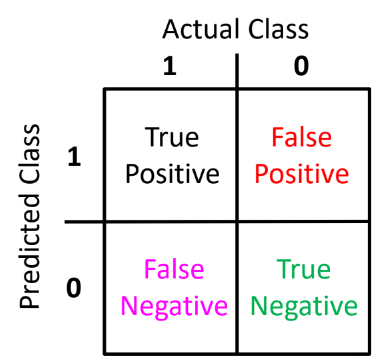


우리는 위와 같은 프리시젼, 리콜 이라는 2개의 measure(측도 -> 측도론에서 배웟던거)을 도입할 수 있다.
각각에 대해선 인공지능개론(정리한 글 링크 : 추후 첨부 예정)에서 공부했으니까, 간단히만 복습하면,
뒤에 단어는 모델이 예측한 거고, 앞에 단어는 그 예측이 실제로 맞았냐 틀렸냐는 거다.
예를 들어, false positive는, 모델이 맞다고(positive라고) 예측했는데, 실제로는 (그 예측이) 틀렸다는 거다. 즉, 맞다고 예측한 게 틀렸으니까, 실제론 아닌(negative인) 것이다.
precision은 "맞은거" / "맞다고 예측한 거" 로, 내가 한 예측이 얼마나 정밀했냐를 의미한다.
recall은 "내가 몇개나 맞혔냐" / "실제로 맞은 것 중에" 로, 현실 세계를 얼마나 재현했냐를 의미한다.
구글 검색 결과로 예시 들어볼 수 있는데, 더 복잡해서 그냥 예제들 스스로 찾아보고 이해하자.
Trading off precision and recall
근데, precision이랑 recall이 둘다 높으면 당연히 좋은 모델인데, 실제론 좀 애매할 수 있음. precision이 높은데 recall이 낮을 수도 있고, 그 반대일 수도 있고. 이런 경우 어느게 더 좋다고 말하기 애매함.
ex. 예를 들어, 암인지 아닌지 예측 모델
- precision이 높다 : 결과 중에 제대로 맞힌 게 많다. 근데, precision을 높이려고 암일 가능성이 적은 건 틀렸다고 봤을 수도 있다. 따라서 암이 맞는데 암이 아니라고 판단받는 사람이 많을 수 있는데(=> false negative가 커져서 recall이 작아짐 -> 즉 recall이 낮을 수 있는데), 이게 precision 값에는 반영이 되지 않는다.
- recall이 높다 : 실제 암인 사람 중에서 많이 내가 맞혔다. 근데, recall을 높이려고 조금만 암일 가능성이 있어도 맞다고 할 수 있다. 따라서 실제론 암이 아닌데 암이 맞다고 판단받는 사람이 많을 수 있는데(=> false positive가 커져서 precision이 작아짐 -> 즉 precision이 낮을 수 있는데), 이게 recall 값에는 반영이 되지 않는다.
예를 들어, 무인자동차의 경우 precision이 높은 것보단 recall이 높은 게 더 나을거임. 조금이라도 문제가 있어보이면 바로 급브레이크 밟아야 하지 않겠음? 사고 위험 낮은 상황이라고 그냥 무시하고 갈 순 없자너.
여기서, 우리가 로지스틱 회귀에서 배웠던 것대로 h가 임계값(Threshold)보다 큰 경우 1을, 작을 경우 0을 출력하도록 모델링을 해보자.
여기서, 만약 내가 정말 암일 확률이 높은 것들만 1이라고 예측한다면, 이건 임계값을 굉장히 높게 잡았다는 거다. 이 경우는 precision은 높게 되고, recall은 낮게 된다. 즉, 실제론 암인데 내가 조심스럽게 하다보니 놓친 비율이 높아진다.
반대로, 실제론 암인데 놓친 경우를 최소화하고 싶어서, 조금만 가능성이 있어도 1일 거라고 예측한다면, 이건 임계값을 좀 낮게 잡았다는 거다. 이 경우는 recall은 높게 되고, precision은 낮게 된다. 즉, 내 판단이 틀린 비율이 높아진다.
이러한 관계를 그래프로 표현하면 아래와 같다. (임계값이 각 recall, precision 값에 대응된다.)

일반적으로, precision과 recall은 위와 같이 반비례 관계. 위 곡선을 precision-recall curve(곡선) 이라고 함.
위 그래프에선 빨강색 선처럼 나타나면 좋을 것임. 그러면 recall이랑 precision 둘다 최대한 좋게 만들 수 있으니까.
우린 이 recall이랑 precision을 동시에 평가하기 위한 measure이 필요함. 경우에 따라 recall이 좀 더 높은 걸 선호하거나 반대를 선호할 순 있어도, 기본적으로 둘다 적당히 크면서 한쪽이 너무 극단적이지 않은 경우가 좋지 않겠음??

precision과 recall을 둘다 반영하기 위해, 단순하게 산술 평균을 생각해보자. column 3에 average 값으로 산술 평균을 쓰고있다.
근데, 저건 precision과 recall이 커져도 그걸 좀 더디게 반영함. 또 precision이나 recall가 극단적으로 값이 차이나는 경우조차도 성능이 괜찮게 나옴. (저건 성능이 나쁘게 나와야함...)
그래서 산술평균이 아닌 F1 score을 사용함. precision과 recall의 조화평균임.
강조) 우리의 목표는, "최적의" 임계값을 찾는 것이고, 각 임계값이 따라 recall과 precision이 생성되는데, "이 임계값이 최적이다 아니다"를 따지는 기준으로, recall, precision이 극단적이지 않으면서 둘다 적절히 큰 값인 경우를 최적이라고 할 거임. 여기서 "둘다 적절히 큰"지 아닌지 판단하기 위해, 두 measure을 한꺼번에 반영해주는 산술평균, F1 score 값을 사용하는 건데, 산술평균은 극단적인 case를 걸러주지 못하므로 F1 score을 사용할 것임.
임계값에 대응되는 recall과 precision이 존재하는 느낌. 정확히는 임계값을 정하고 그걸로 cv set을 분류하고 나면, recall과 precision을 계산할 수 있음.
이러한 measure 중 '곡선 아래의 면적'이 있음. 완벽한 정사각형 면적을 100이라 보고.
이 방법의 단점은 면적 계산에 리소스가 들어간다는 거임. 그래프가 실제론 더 더럽게 나오기에.
여담) yolo 같은 건 mean-average precision(mAP)을 쓰는데, 각 class 별 'precision'의 average을 구한 후, 전체 class를 가지고 각각의 'average precision'의 mean을 구해 measure로 씀. 저걸 쓰면 mAP 값이 90%을 넘기가 힘듦.
여기서 'average precision'이 바로 저 그래프의 아래 면적을 의미함.
결국 실제론 어떤 측도를 사용해 모델을 평가하냐 하면, 일반적으론, precision, recall, error, accuracy, f1 score, mAP 등등 다양한 measure을 다 봄.
Data for machine learning
저번 글 마지막에서 high bias인 경우엔 데이터를 더 수집하는 게 성능을 높이는데 도움이 되지 않는다고 했지만, 대부분의 실제로는 데이터가 많을 수록 도움이 많이 되는 경우가 많다.

다음은 빈칸에 어떤 단어가 들어갈지 예측하는 모델이다. 우리는 4가지의 학습 알고리즘을 사용해, training set 크기에 따라 그 성능(정확도)를 측정했는데, 보면 학습 셋 크기가 커질 수록 성능이 증가하고 있는 걸 볼 수 있다. 또한, 처음에는 성능이 주춤했던 학습 알고리즘도, 학습 셋 크기가 커지니까 성능이 다른 애들보다 더 좋아지기도 한다.
현실에서는 이렇게 좋은 알고리즘도 중요하지만, 그만큼 좋은, 많은 데이터를 잘 확보하는 것도 중요하다.
여기서 우리는 이 피쳐만으로 모델을 구성해도 충분할까? 고민이 될 수 있는데, 이 때는 도메인 전문가한테 물어본다고 가정해보면 좋다. 예를 들어, 위와 같이 빈칸에 들어갈 단어 맞히기 문제의 경우, 원어민이 문제를 맞힌 다 하면 주변 단어들이 feature가 되어 충분히 빈칸에 들어갈 단어를 골라낼 수 있다. 반면에, 집값 문제의 경우 feature가 면적(=feet^2) 하나만 주어진다 하면, 부동산 전문가가 집의 면적만 보고 집값을 잘 예측할 수 있을까?? 아마 쉽지 않을 것이다. 따라서 이 경우는 추가 피쳐가 필요하다.
전 글에서 공부했다시피, 피쳐가 y를 제대로 예측하기에 부족하다면(충분하지 않다면), high bias 문제가 생겨서 데이터 셋을 늘려봐야 별 도움이 안 됐다. 따라서 지금 내가 하려는 예측에 피쳐가 부족하진 않은가 판단하고, 그렇다면 적절한 피쳐를 추가해야 한다.
그렇게 우리가 y를 예측하기에 충분한 피쳐(또는 신경망의 파라미터)들을 가지고 있다고 가정해 보자. 이 경우 우린 강력한 low-bias 알고리즘을 가진 것이다. 이 경우 저번 글의 마지막과 같이, training set size가 충분히 커지면 커질수록 training error(J_test)는 감소했다.
따라서 피쳐(또는 파라미터)가 충분한 경우에는 많은 데이터를 모으는 것이 모델 성능 향상에 도움이 된다.
'AI > 머신러닝(코세라)' 카테고리의 다른 글
| [ML] #11 비지도 학습 - 클러스터링(Unsupervised learning - clustering) (0) | 2024.11.08 |
|---|---|
| [ML] #10 서포트 벡터 머신(SVM, Support Vector Machine) (0) | 2024.11.08 |
| [ML] 신경망으로 이진 분류를 할 때의 결정 경계(decision boundary) 구하기 (0) | 2024.10.18 |
| [ML] chain rule을 이용한 back propagation 공식 유도 손정리 (0) | 2024.10.18 |
| [ML] #8 머신러닝 실사용 꿀팁들(Advice for applying machine learning) (0) | 2024.10.15 |



