본 글은 학교 '머신러닝' 수업을 들으며 공부한 내용을, 저의 말로 바꿔서 남에게 설명해주듯이 쓰는 글입니다.
다시 한번 복습하는 과정에서 Coursera Andrew Ng 교수님의 강의를 일부 수강하였고, 인터넷 검색 등을 통해 내용을 보충하였습니다.
너무 쉬운 개념들은 따로 정리하지 않았습니다. 따라서 해당 글에는 적히지 않은 개념들이 일부 있을 수 있습니다.
본 글은 Andrew Ng 교수님의 'machine learning' 수업 강의 노트를 일부 사용하였습니다.
본 글에 사용된 강의노트 사진들 대부분의 저작권은 'DeepLearning.AI'에 귀속되어 있음을 밝히며,
본 글은 'DeepLearning.AI'의 'Copyright rights'에 따라 수익 창출을 하지 않고,
또한 해당 정책에 따라 '개인 공부 및 정보 전달'이라는 교육적 목적으로 글을 작성함을 밝힙니다.

The problem of overfitting
@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@
주의!!
제목에 '정규화(regularization)'라고 적긴 했지만, normalization과 번역이 같아 헷갈릴 수 있음.
그래서 본인은 이 블로그 안에선 regularization을 '리규화' 라고 내 마음대로 지칭할 것임.
@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@

세 그래프 다 주어진 data set은 동일함. (점이 동일하게 찍혔으니까)
왼쪽 : underfitting이 발생함. h가 data set에 적합하지 못함. "High Bias" 라고도 부름.
가운데 : just right
오른쪽 : overfitting이 발생함. h가 data set에 과적합함. "High Variance" 라고도 부름.
다항 회귀를 사용하면 오른쪽과 같이 Sigma(error) = 0이 되도록 설계가 가능하나, 저렇게 값이 튀기도 하고 막 이상해져서 과적합이 발생함. 기존의 data set들에 대해서는 굉장히 잘 들어맞지만(error가 거의 없지만) 새로운 data를 generalize하기 어려움.
** generalize를 잘 한다 : 가설(h)이 새로운 data에 잘 적합(fit)하다.

logistic regression 예시를 보자. 오른쪽을 보면 억지로 저 data set에 fit하려하니까 항을 계속 추가할 수밖에 없어진다.
여기서, 저런 label이 튄 부분은, labeling 실수일 수도 있다. labeling도 기본적으론 사람이 하니까. 근데, 저런 label 실수가 1000개 있다면? 저거 다 맞출거냐?
실제론 저런 noise에 model을 다 맞출 필요는 없다. 가운데처럼 적당히 하면 됨.

만약 feature가 하나라면, 위와 같이 data set을 점으로 표시하고, observation - prediction 그래프를 그릴 수 있음. 이렇게 그림을 그려보고 overfitting인지 아닌지 판별할 수도 있음.
그러나, feature가 늘어날 경우 그림으로 그리기는 굉장히 어려워짐.
또한, 여기서 그 이유를 서술하진 않겠으나, 일반적으로 dimension이 늘어나는데 training set이 충분히 늘지 않으면 overfitting이 발생할 수 있음.
(그 이유에 대해선 https://for-my-wealthy-life.tistory.com/40 여기서 이해하기 쉽게 설명해주고 있음.)

그렇게 과적합이 발생했을 때, 두 가지 방법이 있는데
1. feature 개수를 줄인다.
꼭 필요한 feature들 위주로 keep함. 이 과정에서 선택 알고리즘이 쓰이기도 함.
2. 리규화를 한다.
feature 개수는 유지하되 그 값의 크기를 줄임. 각 feature들이 하나하나 소중할 때 하면 좋음.
cost function
이번엔 cost function에 리규화를 적용해보자.

좌측의 그래프가 just fit 그래프이고, 우측의 그래프가 overfitting된 그래프라 해보자.
두 그래프 식의 비교해보면, 우측의 x^3과 x^4 항을 없애면 왼쪽처럼 될 것이다.

이를 위해, 위 J의 오른쪽에 쎄타3과 쎄타4에 큰 수를 곱한 값을 더해보자.
그리고 이 상태로 gradient descent를 돌린다고 상상해보자.
J가 최소화되는 쪽으로 점이 이동해 쎄타 값이 정해질 텐데,
이 때 J 그래프에서 쎄타3과 쎄타4 값이 큰 곳들은 J값이 어마무시하게 위로 솟구칠 것이므로 그 쪽으로는 수렴하지 않을 것이다.
따라서 최종적으로 수렴된 점은 쎄타3과 쎄타4 값이 매우매우 작은 지점일 것이다. 이를 파라미터에 패널티를 부여한다고 한다.
이는 x^3과 x^4가 거의 영향력이 거의 사라져, 좌측과 같은 2차 함수 꼴에 근사한다.

방금까진 특정 영향력이 큰 파라미터에만 패널티를 부여했지만, 이번엔 모든 파라미터에 패널티를 부여하면 어떨까?
이렇게 하는 이유는, J를 좀 더 간단하게 구해보고 싶어서다.
일반적으로 이렇게 파라미터를 작게 하면 그 부분들이 부드러운 곡선으로 변한다.
모든 파라미터에 패널티를 부여하면 그 곡선이 전체적으로 부드럽게 변할 것임.

그렇기에, 위 식의 오른쪽처럼 리규화 항을 정의해보자.
이제 모든 파라미터에 대해 패널티가 적용된다.
여기서, 쎄타0을 리규화하지 않는 이유는, 쎄타0에 곱해지는 x^0은 어차피 1이니까 리규화를 해줄 필요가 없기 때문이다.
(x는 training set으로 주어지는 값, 쎄타는 내가 gradient descent로 구해내는 값임을 잊지 말자!!)

참고로, 리규화 텀으로 제곱을 사용하는 이유에 대한 gpt의 답변은 위와 같다.

이러한 리규화는 잘만 쓰면 h가 과적합하는 걸 막아줘서 유용하다.
그러나, 만약 위와 같이 람다가 엄청 큰 수가 들어갔다 하면 어떻게 될까??
그러면 쎄타0을 제외한 모든 파라미터들이 0에 근사할 것이고, 결국 h는 x값에 상관없이 쎼타0에 근사한 직선 형태를 띠게 된다.
이는 underfitting 되었으며, strong preconception과 high bias를 가진다.
따라서, 그 사이 적절한 람다값을 설정하는 것이 중요하다.
람다가 크면 : underfitting 발생 가능.
람다가 작으면 : overfitting 발생 가능.
Regularized linear regression
이제, 선형 회귀에서 regularization이 어떻게 적용되는지 살펴보자.

복잡해 보일 수 있으나... 정규화 텀은 j를 고정시켜뒀을 때니까 미분하면 저렇게 추가되는 거고
마지막 줄은 그냥 식을 정리한 것 뿐.
쎼타0일 땐 리규화를 부여하지 않기 때문에 따로 빼준 것 주목하자.
(잊지 말자!! 쎄타는 초기값부터 계속 update 되어가는 거임. 그리고 x는 주어짐!!)
마지막 식의 결과는 꽤나 흥미로운데, 비교를 위해 선형 회귀때의 식을 가져와보자.

차이가 보이는가?
선형 회귀때에 비해, 앞부분에 쎄타j 부분에 1 - alpha * 람다 / m 이 추가되었다.
그리고 뒤에 learning rate 항은 똑같다.
여기서, 1 - alpha * 람다 / m 는 1보다 아주 약간 작은 수가 된다.
alpha는 매우 작고, m은 보통 매우 크며, 또한 모두 양수이기 때문이다.
0,99와 같은 수가 될 수 있다. 즉, 쎄타j를 살짝 더 작게 만든다.
쎄타j를 살짝 작게 만들고, 그 후 기울기를 빼주는 걸 반복하면 된다.
여기선 뒤에 꺼 항 영향을 더 많이 받는다는 걸 알 수 있다.

정규 방정식에도 리규화를 적용 가능하다.
우리가 기존에 봤던 정규 방정식을 통해 구한 쎄타는 위와 같다.

그리고, 위는 리규화된 정규 방정식이다. (증명은 생략함.)
참고로, m <= n 인 경우 (data set보다 feature 개수가 더 많은 경우), X^T*X가 singularity일 수 있는데, 이게 리규화하면 해소된다.
Regularized logistic regression
이제 로지스틱 회귀에 리규화를 적용해보자.

오른쪽과 같이 g가 시그모이드고 z가 고차 poly식일 때, 왼쪽 파란 선과 같이 overfitting 될 확률이 높다는 건 이미 다뤘다.
이 경우, 아래처럼 cost function이 나올 것이다.
이제, 여기에 규화를 적용하면 어떻게 될까??
그 decision boundary는 분홍 선이 될 것이고, 리규화 텀은 아래와 같다.

그리고, 이를 gradient descent를 위해 미분하면, 아래와 같다.
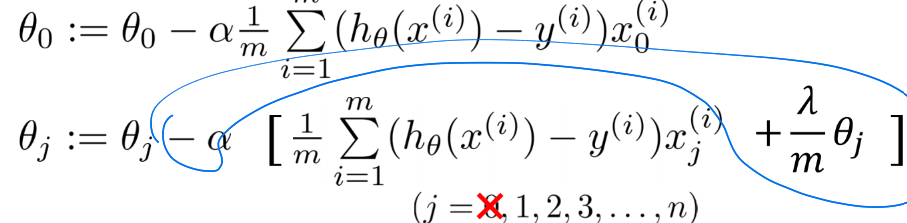
이는 선형 회귀때의 식과 동일하다.(당연)
(물론, 1 - alpha * 람다 / m 꼴로도 변형 가능)
'AI > 머신러닝(코세라)' 카테고리의 다른 글
| [ML] #7 역전파(Backpropagation) (0) | 2024.10.15 |
|---|---|
| [ML] #6 신경망(Neural Networks) (0) | 2024.10.15 |
| [ML] #4 로지스틱 회귀(Logistic Regression) (0) | 2024.10.14 |
| [ML] #3 다변수 선형 회귀(Linear Regression with Multiple Variable) (0) | 2024.09.20 |
| [ML] #2 일변수 선형 회귀(Linear Regression with One Variable) (0) | 2024.09.19 |



