본 글은 학교 '머신러닝' 수업을 들으며 공부한 내용을, 저의 말로 바꿔서 남에게 설명해주듯이 쓰는 글입니다.
다시 한번 복습하는 과정에서 Coursera Andrew Ng 교수님의 강의를 일부 수강하였고, 인터넷 검색 등을 통해 내용을 보충하였습니다.
너무 쉬운 개념들은 따로 정리하지 않았습니다. 따라서 해당 글에는 적히지 않은 개념들이 일부 있을 수 있습니다.
본 글은 Andrew Ng 교수님의 'machine learning' 수업 강의 노트를 일부 사용하였습니다.
본 글에 사용된 강의노트 사진들 대부분의 저작권은 'DeepLearning.AI'에 귀속되어 있음을 밝히며,
본 글은 'DeepLearning.AI'의 'Copyright rights'에 따라 수익 창출을 하지 않고,
또한 해당 정책에 따라 '개인 공부 및 정보 전달'이라는 교육적 목적으로 글을 작성함을 밝힙니다.

로지스틱 회귀(Logistic Regression)

이제 예측하려는 변수 y가 이산적인 값을 가짐. 분류는 이진 분류와 다중 클래스 분류로 나뉘는데, 일단 우리는 이진 분류(binary classification)만 다룰 것임. 즉, y가 0 또는 1임.
0 : negative class
1 : positive class
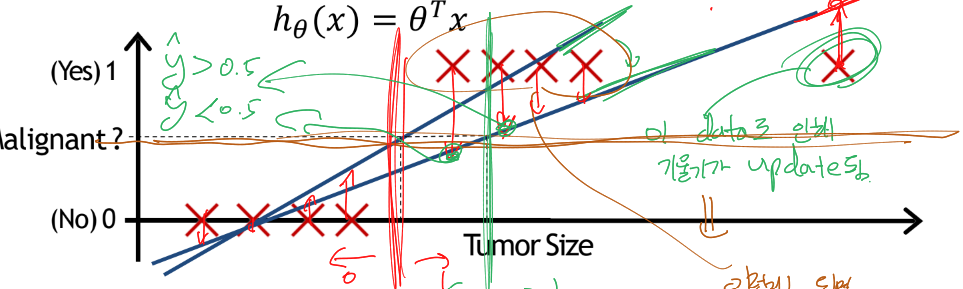
복잡해보일 수 있다. 일단 다 제쳐두고, 왼쪽부터 점 8개에 대한 일차 선형 회귀식을 구해보자. 왼쪽의 직선과 같이 그려진다.
이제, 임계값을 y-hat (즉, h) = 0.5로 두고, 그보다 크거나 작으면 y가 1이라고, 그보다 작으면 y가 0이라고 예측하는 분류 모델을 생각해보자. 즉, 저 선형 회귀 직선의 함수값을 말하는 거다. 위의 그림의 세로 빨간 선이 그 경계가 된다.
저 빨간 선보다 왼쪽에 있는 size가 관측되면 암이 아니라고 함.
처음에는 꽤나 잘 예측하는 걸로 보인다.
그러나, 오른쪽 끝에 저 data가 새로 추가됏다. 이제 일차 선형 회귀 식이 (즉, h가) 기울기가 완만하게 바뀐다. 이젠 y-hat = 0.5 일 때를 threshold로 두면, 저 초록 세로 선이 경계가 되고, 왼쪽에서부터 5번째 x에 대한 예측이 1에서 0으로 바뀌게 됐다.
같은 환자를 처음에 암이라 분류했다가, 다른 환자가 들어와 내 예측식이 바뀌니까 이젠 암이 아니라고 분류하는 것이다.
만약 저렇게 분류하는 병원이 있다면 망할거다(ㅋㅋ...)
즉, 분류 문제에 선형 회귀를 사용하는 건 좋지 않다.

또한, 선형 회귀를 써버리면 h가 0~1 사이 범위를 뚫고 나갈 수 있다. 이론상 h는 -infinity ~ +infinity 가 가능하다. 이게 뭐 문제냐? 할 수 있지만, 이러면 확률 형태로 표현이 힘들게 된다.
자세히 말하면, 우리가 이진 분류를 0 or 1로 한 건, 확률상 0 or 1 값을 부여한 것이다. P 가 1이란건 무조건이란 거고, 0 이란 건 아니란 거다.
예를 들어, h가 80이 나왔으면, 이 사람은 80% 확률로 암에 걸린 것이다. 그렇기에 우리는 y = 1, 즉 암에 걸린 게 맞구나! 하고 예측이 가능하다.
그러나 h가 120이 나오면? 980이 나오면? 980% 확률로 암에 걸렸다고 하면 확률의 정의상 말이 되지 않는다.


우리가 써왔던 선형회기 식이 저기 왼쪽에 h = 쎄타^T * x 이다. 근데 이걸 하니까 범위가 막 늘어나니까 문제가 됐자너. 그러니까, 겉을 적당한 함수로 하나 씌워줄건데, 그 g(x)를 시그모이드(sigmoid) 함수를 쓸 거임.

시그모이드 함수는 요렇게 생김. 어떤 x가 들어오든 0~1 사이의 함수값을 반환함.

앞서 설명했듯이 h = 0.7 -> 70% 확률로 양성(1) 이라는 뜻.
h는 P(y=1 | x; 쎄타) 라고도 표현함. 해석하면, x가 주어지고, 파라미터가 쎄타 일 때, y = 1일 확률은? 이다. h와 일치함.
반대는 즉 1 - h는 P(y=0 | x; 쎄타) 가 되지용.
Decision boundary

우리의 시그모이드 함수 g는 저렇게 생김.
그리고 z = 쎄타^T * X임.
h 즉 g가 0.5보다 크거나 같으면 양성인 거니까
다르게 말하면 속함수인 z가 0보다 크거나 같으면 양성임.

예를 들어, 쎼타를 순서대로 -3, 1, 1이라고 가정하면, decision boundary는 왼쪽과 같이 됨. 당연.
즉, 쎄타가 decision boundary를 결정하고, 쎄타는 data set을 통해 학습해서 얻어냄
정리) data set로 학습시킴 -> 쎄타 값 얻어냄 -> decision boundary 특정

아까는 linear decision boundary가 생긴 경우였고,
지금은 non-linear 한 경우.
아래처럼 복잡한 decision boundary의 경우 우측처럼 poly의 차수를 높여 표현 가능.
기본적으로,
z 가 linear -> decision boundary도 linear
z가 non-linear -> decision boundary도 non-linear 이다,
Cost function
아까 세타가 decision boundary를 정한다 했고, data set이 쎄타를 정한다 했자나.
이제 쎄타를 구하는 법을 알아보자.
쎄타는 어떻게 구하지? gradient descent를 구해야 한다.
그리고 이를 위해선 먼저 cost function을 정의해야 한다.


아까 정의한 h를 그대로 y-hat으로서 MSE에 때려박아버리면, 왼쪽처럼 non-convex(볼록하지 않은 함수)가 된다.
이러면 global minimum에 수렴하기 좀 성가시당...
오른쪽 꼴의 convex한 함수로 J가 나왔음 좋겠따!!

따라서, 우리는 기존에 쓰던 MSE가 아닌, 이러한 다른 비용 함수를 사용할 것이다.
이 비용 함수를 사용할 때 어떤 특징이 있는지 살펴보자.

우선, label이 이미 주어진다는 것에 주의하자. y = 1로 이미 주어진 상황이다. 즉, 이미 이 환자는 양성인 상황이다.
주목해 볼 점은, y = 1 이고 h = 1인 경우, 즉 의사가 양성인 환자를 양성이라고 예측했을 경우, cost = 0이 된다.
또한, y = 1이고 h -> 0인 경우, 즉 의사가 양성인 환자를 음성이라고 예측했을 경우, 어마무시한 cost가 부여된다.

y = 0일 경우이다. (왜 저런 h그래프가 유도되는지는 생략함)
주목해 볼 점은, y = 0 이고 h = 0인 경우, 즉 의사가 음성인 환자를 음성이라고 예측했을 경우, cost = 0이 된다.
또한, y = 0이고 h -> 1인 경우, 즉 의사가 음성인 환자를 양성이라고 예측했을 경우, 어마무시한 cost가 부여된다.
또한, y 값에 상관없이, h = 0.5일 경우 cost는 −log(0.5)≈0.693 로 같은 값이 나온다는 것도 알아두자.
Simplified cost function and gradient descent

아까 y = 1, y = 0인 경우로 case를 나눴지만, 딱 저 두 case만 가정했기 때문에 저 저렇게 정의하면 한 식으로 나타낼 수 있다!!

대입하면, J는 위와 같다.
이제 편미분한 값을 구해보자.
우선, 시그모이드 함수를 미분하면 다음과 같다.

(어차피 과정은 쉽게 유도 가능하니, 결과만 외우자 일단.)
따라서, 여러 미분 과정을 거치면 (과정 생략, 강의노트 참고)

다음과 같은 결과가 나온다.
(암기 : error * x 를 시그마 씌운 꼴)

최종적으로, 위와 같이 gradient에 learning rate alpha를 곱한 값을 빼주면 gradient descent 식이 완성된다.
놀라운 점은, 선형 회귀때와 그 식이 같다는 거다!!
아래는 선형 회귀때의 식이다.(정확히 모양이 일치한다.)
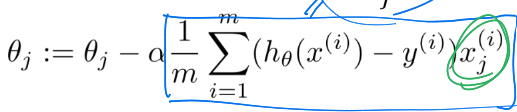


여담이지만, 실제로 매트랩이든 파이썬이든 코드를 짠다면
좌측처럼 행렬 요소 하나하나 반복문을 돌리기보단
우측처럼 벡터 단위로 연산하는 것이 더 성능이 보통 더 좋음.
Advanced Optimization
비용 함수의 최소값을 찾는 방법들 중 gradient descent 말고 다른 방법들을 몇 가지 알아볼 것임.

왼쪽 아래에 저 3가지가 좀 더 최적화된 방식들인데, 장단점이 있음.
장점 : alpha를 직접 내가 고를 필요가 없음. 원래는 a를 0.01 이런 수로 내가 임의로 지정해줘야 했자너. 근데 얘는 얘가 알아서 alpha를 선택함. 또한, 종종 그냥 gradient descent보다 더 빠르게 최솟값으로 수렴함.
단점 : 더 복잡함. 다만, 실제로는 그냥 대충 이해만 하고, 라이브러리 딸깍! 함수 딸깍딸깍! 해서 쓰면 됨.
결론 : 저런 게 있다~~ 알고 넘어가기.

참고로, 실제로 코드로 구현한 다 했을때, gradient descent 연산 자체에 대해서는 J를 편미분한 값만 계산해서 update해나가면 됨. 그러나, 실제로는 J값 또한 계산하게 되는데, 이건 number of iterations 에 따른 J 값을 시각화해서 수렴이 잘 되고 있는지 확인하려는 것임.

매트랩으로 cost function 부분을 구현한다면 우측과 같을 것임.
참고만 하고 넘어가자 일단.
Multi-class classification : One vs all

위와 같이 현실엔 분류 결과 class가 두 개가 아닌 여러개인 경우도 있음.

우리가 기존에 해온 이진 분류(좌측)과 달리, 여러 class들이 기호로 표시된 모습(우측).
우리가 궁금한 건, 새로운 data가 들어왔을 때, 이게 어느 class에 속할 지인데, 이걸 어떻게 알아낼 수 있을까?
이 알아내는 방법에는 여러가지가 있지만, 그 중에서 one-vs-all 알고리즘을 사용해 해결하는 방식을 알아보자.

위와 같이 class 하나를 고정시켜놓고, 그 class vs 나머지 모든 class로 나눠서 그 data set들로 쎄타를 구하고, 쎄타를 알고 있으니 h의 식과 decision boundary도 자동으로 구해진다.

그렇게 하면 각 class에 대한 h 식이 나오게 되고, 여기에 새로운 data 의 feature 값들만 집어넣어주면 h값이 상수로 정해져서 나오게 된다.
그러면 이제 상수값인 h값들을 비교해서, 가장 큰 h값을 가지는 class의 경우가 그 data의 class라고 보면 된다.
(설명하다보니 말이 좀 꼬였는데, 왜 data set을 알면 쎼타를 알고, 왜 쎄타를 알면 h식의 꼴을 알 수 있다는 건지는 아까 로지스틱 회귀 초반부의 h 식을 참고하자.)
여기선 간단하게 one - vs - all을 여러번 사용하는 방식으로 multiclassification을 하긴 했지만,
실제론 그냥 softmax 함수를 써서 확률 분포를 가지는 벡터 형식으로 출력하면 된다.~~
참고로, "multi-class에 대해, 새로운 data가 어느 class에 속할 지 예측하는 방법" 에는 우리가 이번에 다룬 one-vs-all 이외에도 이런 방식들도 있다.
- KNN
- decision tree
- 신경망
- naive bayes
다다음 챕터에서 배울 신경망을 제외하곤 인공지능 입문과정 수업에서 배웠던 방법들이다.
필요하면 강의노트 찾아보면서 복습하장.
'AI > 머신러닝(코세라)' 카테고리의 다른 글
| [ML] #6 신경망(Neural Networks) (0) | 2024.10.15 |
|---|---|
| [ML] #5 정규화(Regularization) (0) | 2024.10.15 |
| [ML] #3 다변수 선형 회귀(Linear Regression with Multiple Variable) (0) | 2024.09.20 |
| [ML] #2 일변수 선형 회귀(Linear Regression with One Variable) (0) | 2024.09.19 |
| [ML] #1 머신러닝 개론(Introduction to Machine Learning) (0) | 2024.09.19 |



