본 글은 학교 '머신러닝' 수업을 들으며 공부한 내용을, 저의 말로 바꿔서 남에게 설명해주듯이 쓰는 글입니다.
다시 한번 복습하는 과정에서 Coursera Andrew Ng 교수님의 강의를 일부 수강하였고, 인터넷 검색 등을 통해 내용을 보충하였습니다.
너무 쉬운 개념들은 따로 정리하지 않았습니다. 따라서 해당 글에는 적히지 않은 개념들이 일부 있을 수 있습니다.
본 글은 Andrew Ng 교수님의 'machine learning' 수업 강의 노트를 일부 사용하였습니다.
본 글에 사용된 강의노트 사진들 대부분의 저작권은 'DeepLearning.AI'에 귀속되어 있음을 밝히며,
본 글은 'DeepLearning.AI'의 'Copyright rights'에 따라 수익 창출을 하지 않고,
또한 해당 정책에 따라 '개인 공부 및 정보 전달'이라는 교육적 목적으로 글을 작성함을 밝힙니다.


모델 표현(model representation)
우선, notation 정리부터 하자.
m = 트레이닝 예시들의 수
x = input variable / features (입력 변수 / 피쳐)
y = output variable / targat(s) (variable) (출력 변수 / 타겟 (변수) )
(x, y) = 하나의 트레이닝 예시 / 데이터 셋
( x^(i) , y^(i) ) = i번째 트레이닝 예시 (이때 i는 1부터 시작함. 프로그래밍이랑 다르다~~)
**참고로, 위첨자를 'superscript'라고 하고, 데이터 셋에 주로 사용됨.
아래첨자는 'subscript'라고 하고, parameter에 주로 사용됨.


Learing process
머신러닝은, "Training Set 으로 Learning Algorithm을 돌리고, 이를 통해 hypothesis(가설)의 식에 대한 '최적의' parameter을 찾는 과정"이라고 할 수 있을 것 같다.
여기서 중요한 건 h는 일종의 함수 내지 E 꼴이라는 것이다.
예를 들어, 우리가 다룰 일변수 선형 회귀 가설의 경우는 h(x) = θ0 + θ1x로 표현 가능하다.
여기서 θ0, θ1가 h의 parameter다.
이 때, training set은 우리가 구축해야 하는 대상이며, 내 data sets들에 따라 어떤 Learning algorithm을 선택할 지도 우리가 결정해야 한다.
일단 학습을 완료하고 난 뒤부터는 Training set이랑 learning algorithm 주렁주렁 달고 다닐 필요 없이 h만 가지고 다니면 돼서 매우 편리하다.
보통 training set이 많으면 100gb가 넘어가기도 한다고 그러는데, 그에 비해 h는 1gb정도밖에 안되는 등 용량이 대폭 줄어들어 휴대성이 높다.
(또한, training set이랑 learning algorithm은 기업의 비밀... 그게 공개돼서 좋을 게 없긴 하다.)
비용 함수(cost function)

위와 같이, θ0과 θ1의 값에 따라 h는 다양한 형태의 그래프를 그리게 된다.
잠깐!! 우리가 궁극적으로 뭘 하고자 하는 지 잊은 건 아니겠지??
저 위에 3개의 그래프에는, 데이터 셋이 찍혀있지 않음!
우리의 목적은, observation과 prediction의 차이, 즉 error을 최소화하는 것이고,
또한 결국 그 error을 최소화해주는 h의 parameters을 구하는 것임!!
근데, 어떻게 error을 최소화 할거야??
뭐 말은 좋은데, error이란 건 값의 차이 아니야? 근데 값이 여러갠데 뭘 어케 뺄건데?
=> "Least Square Method"를 사용하여 "Mean Squared Error"을 최소로 하는 θ0, θ1을 구하자!!!!
(LSM과 MSE가 뭔지 잘 모르겠다면 확률 및 통계를 복습하고 오자!!)


**확률 및 통계에서 공부했던 내용을 떠올려보자!!
error을 평균내서 구하는 방법에는 여러가지가 있다.
근데 그 중에 제곱을 씌우는 이유는, 제곱을 안 씌우면 error가 음수가 될 수 있어 더했을 때 그 값이 0에 가까워지기에 유의미한 결과가 나오지 않으며,
그렇다고 절댓값을 씌워버리면 미분이 안되기 때문이다.
또한 세제곱 이상을 씌울 수돈 있지만... 굳이? too much~~~~
(참고로, 분모에 1/2m에 2는 미분할 때 계산 편하라고 달아둔 거다.)

결국 아래와 같이, 식이 나오고, 우리는 저 argmin 식을 J(θ0, θ1)이라고 정의하여 '비용 함수(cost function)'이라 부르기로 할 것이다.
왜 비용 함수냐고?? 그야 저 식의 값에 비례하는 정도로 error가 생길 것이고, error가 생긴다는 건 비용을 치룬다는 거잖아?
그리고 저 J(θ0, θ1)을 최소로 만드는 θ0, θ1을 구하게 되면, 결국 그게 우리가 궁극적으로 원하던 "error가 최소가 되게끔 하는 parameter 찾기"를 달성하는 것이다.
즉, 우리의 목적은 "J값이 최소가 되는 지점을 찾는 것"이다. 어디서 많이 본 목적 아닌가?? 맞다, 미분적분학에서 지겹도록 하던 '최솟값 찾기'이고, 이는 높은 확률로 '극소값'이 된다. 따라서 우리는 해당 J함수를 미분해서 최솟값을 찾아낼 것이다.
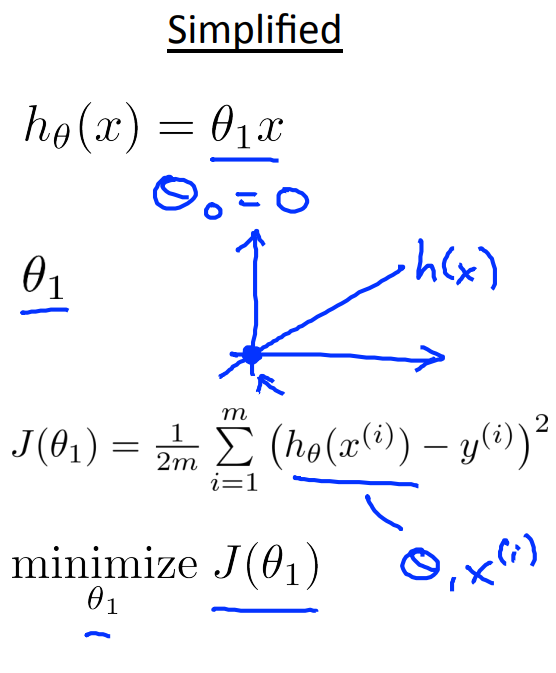
이제, 단순화해서 관찰해보자.
θ0 = 0을 넣고, J를 일변수함수로 관찰하는 것이다.
그러면 아래 그림들과 같은 모습이 나온다.
(θ1에 직접 값을 대입해 J함수의 모양을 유추할 수 있다. 계산생략)




그런데... 방금 관찰한 건 단순화된 거고, 우리가 실제로 봐야할 건 θ0 가 0이라고 단순화할 수 없는 모델이다.
그럼, J(θ1)이 아닌 J(θ0, θ1)은 어떻게 그려질까??
이는 벡터미적분학에서 배웠던 대로, 두 개의 변수를 가지는 방정식 꼴이 된다.

결국, 이 그림에서 저 볼록하게 튀어나온 극소점의 (θ0, θ1) 쌍을 찾으면, 그게 바로 우리가 원하는 parameter이다.


위는 이 h와 J 함수를 각각 2차원 그래프에 나타낸 것인데,
위의 그래프는 J가 최솟값에서 많이 떨어져 있는 모습이고,
아래 그래프는 J가 딱 최솟값을 가리키고 있는 모습이다.
보면 J가 최소일 때 h의 그래프도 데이터 셋들과 error가 최소가 되는 느낌으로 그려져 있다.
지금까지는 "J가 최소일 때 h의 parameter가 우리가 원하는 최적의 parameter가 된다"는 걸 보여주기 위한 과정이었다.
경사 하강법(Gradient descent)

여기서 data set m개, parameter n개인 그래프를 상상해 볼 수도 있다. 다만 일단은 J의 좀더 일반화된 모습을 상상해 보자.
우리가 방금 다룬 J는 굉장히 예쁜 오목한 형태였다. 그러나 현실의 문제들은 cost function이 그렇게 예쁘진 않을 것이다.
우리가 구한 cost function이 다음과 같다고 가정해 보겠다.


아까 우리는 J를 MSE로 썼지만, 여기는 다른 복잡한 J를 쓴 것이다. 현실 세계의 문제는 아까보단 지금의 manifold(다양체)에 가까운 J가 나올 것이다.
여기서 저 J의 최솟값을 구하기 위해 쓰는 방법 중 하나가 Gradient descent(경사 하강법)이다.
이는 임의의 시작점 (θ0, θ1)에서 시작해서, J의 최솟값을 향해 계속 값을 수정해나가는 방식이다.
예를 들어, 첫 번째 그림에서는 8번 만에 최솟값에 도달하였다.
그런데, 뭔가 이상하지 않는가? 두 번째 그림에서는, 첫 번째 그림과 전혀 다른 최솟값이 도달하였다.
아니 근데, 최솟값이 두개라고? 뭐지??
진정해라.
첫 번째 그림은 global minimum에, 두 번째 그림은 local minimum에 떨어진 것이다.
이와 같이 시작점이 어디냐에 따라 local minimum에 떨어질 수도 있는데,
이 경우는 우리가 구하려던 "J의 (사실상 global) minimum인 case"가 전혀 아니므로 실패한 경우이다.
즉, starting point가 어디냐에 따라 우리가 구한 model의 parameter가 달라질 수 있다는 것인데,
저 모델을 한 번 훈련시키는 데 몇주가 들고 비용도 많이 들기도 하기 때문에
실제로는 starting point를 여러 번 바꿔가며 시도해가는게 아닌, 다른 여러 방법들을 사용해 최대한 local minimum에 빠지지 않도록 유도한다고 한다. (대략 80%의 모델들이 훈련시킬 때 random starting point를 사용한다는 것 같은데 아닐수도 있다.)
그 방법 중 하나가 learning rate 를 건드리는 건데, 조금 뒤에 설명하겠다.

위 수식들이 gradient descent가 실제로 어떻게 작동하는 지 나타내주고 있는데, 여기서 a(알파)는 learning rate 라고 한다.
우리는 J를 각 parameter에 대해 편미분한 것을 a에 곱하고, 그걸 동시에 한번 더 해서 update해줄 것이다.
즉, 현실에서 θ0이랑 θ1을 동시에 update할 순 없지 않는가? 축 하나씩 할 수밖에 없다는 것이다.
이때, 우측 아래처럼 연속적으로 하면 절대 안되고, 좌측 아래처럼 동시에 update해주어야 한다. 이유는 당연히 논리상으론 동시에 update되는 것이 맞기 때문이다.
그렇게 저 J가 수렴할 때까지, 즉 값의 유의미한 변화가 없어질 때까지 for문을 돌리면 된다.
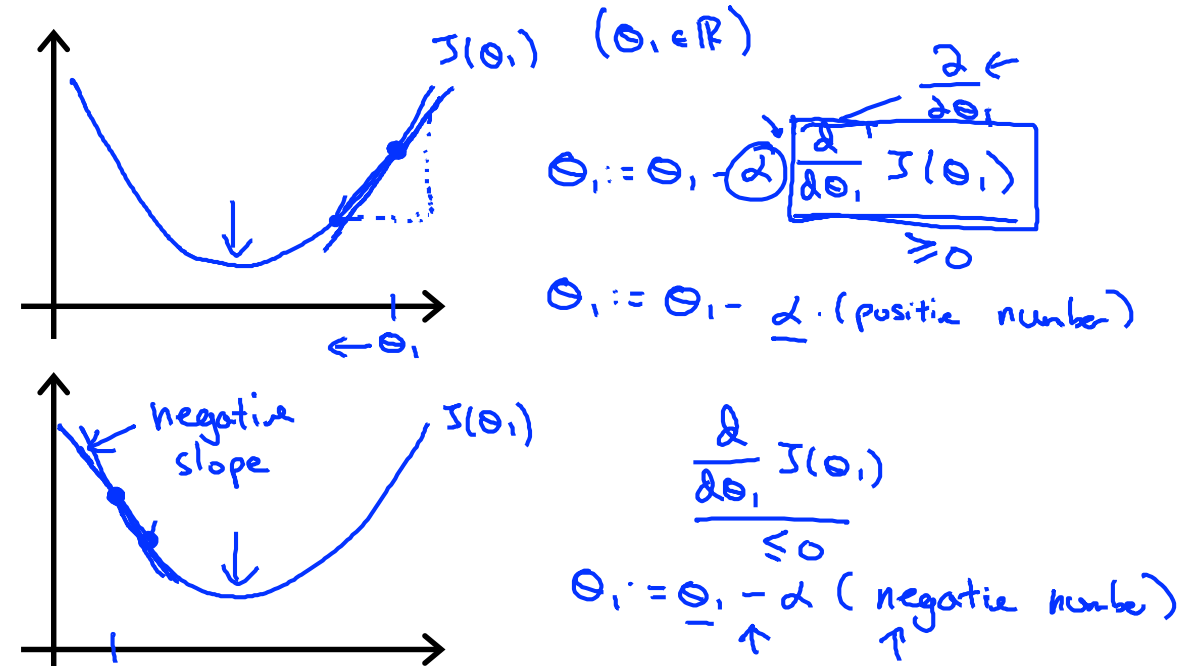
그럼, J가 어떻게 수렴하게 되는 것일까? a의 역할은 뭐고, 왜 편미분한 것 왼편엔 '-' 부호가 붙을까?
그건 위 그림을 보면 이해할 수 있다.
위 그림은 간단하게 J(θ1)의 사례를 본 건데,
J가 최솟값보다 오른편에 있을 때는 그 기울기가 양수이다. 반대로 왼편에 있을 때는 기울기가 음수이고.
그렇기에 오른편에 있을 때는 양수인 기울기에 '-'부호를 붙여 왼편으로, 즉 최솟값에 더 가까워지도록 움직이게 조종하고,
그 반대의 경우도 비슷하게 조종하는 것이다.

여기서, a의 역할을 아직 설명 못했는데,
a값이 작으면 최솟값에 너무 천천히 수렴하고,
a값이 크면 최솟값에 너무 빠르게 다가가는 나머지 폴짝폴짝 뛰어넘어 발산해버릴 가능성이 있다.
그렇기에 적당한 a값을 선정해야 한다.

보다시피, 한번 local minimum에 빠져버리면 기울기가 0이 돼서 절대 다신 빠져나올 수 없다...

이 때 a값이 고정된 값이라 하더라도, 최솟값에 가까워질수록 기울기의 절댓값 자체가 줄어드므로, 점점 수렴하는 속도는 느려진다.
여기선 a(learning rate)에 대한 여담인데,
일반적으로 모델 학습시킬 때는 초기엔 a를 크게, 이후엔 a를 작게 준다고 한다.
초기에 a를 크게 주는 이유는, 우리의 starting point는 믿을 수 없는 point이기 때문이다. 가만히 냅뒀다가 local minimum으로 빠져버릴 가능성이 있다. 근데, a가 충분히 크면 local minimum이어도 성큼성큼 뛰어넘고 진짜 global minimum으로 갈 확률이 늘어난다.
이후에 a를 줄이는 이유는, 후기에는 global minimum 근처로 가 있을 확률이 높으니까 그렇다고 한다.
사실 보통은 local minimum에 잘 빠지진 않고, 오히려 converge가 잘 안 돼서 문제라고 하는데,
영상과 같은 분야는 data 크기가 크다보니 특히 잘 안빠지나
의료쪽 같이 data 값이 작은 곳들은 잘 빠질 수도 있을 것 같다.
그러면, 절대 안빠지게 할 수 있는 방법이 없을까?
=> 가속도를 도입하면 된다.
가속도를 도입하면 값이 웬만해선? 0이 되진 않는다. 기울기가 0이어도 기울기의 변화량은 0이 아니기 때문이다. (0이 될 가능성이 아예 zero인 건지는 모르겠다..)
그러나 이는 수렴 속도를 느리게 만들 수 있고, overshooting(폴짝폴짝 뛰어넘어서 J값이 오히려 커지는거)이 더 많이 일어날 수도 있으니 그리 좋다고 보기도 어렵다.
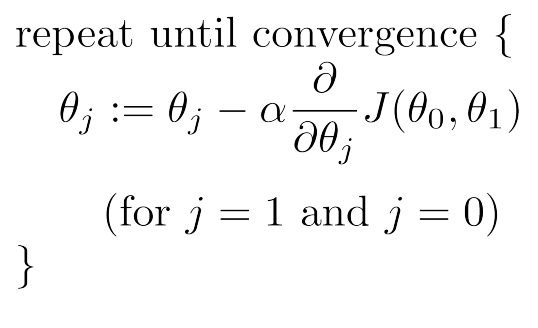
이때, 우측에 나와있는 것처럼 수렴할 때까지 (즉, 값의 변화가 일정 횟수 이상 없을 때까지) 돌려주어도 되나,
실제 머신러닝에서는 "반복 횟수를 직접 정해주는" 방식을 더 선호한다고 한다.
그 이유는 여러가지가 있으나 기본적으로 max iteration 하고(반복횟수 정해주고) a 값을 점점 낮춰주는 방식으로 하니까 기존 모델보다 성능이 더 좋아지기도 하고,
수렴했는 줄 알았는데 더 돌려보니 그게 local minimum이었고 더 돌려서 그걸 빠져나올 수 있었다 이런 이유도 있다곤 하는 것 같다.(이건 확실치 않음)


그리고 미분하게 되면 저런 식이 나오게 되므로,
아까 편미분 그 식에 저 식을 대입해주면
최종적으로 두 번째 사진과 같은 모습이 된다.

우측 그래프의 점들이 gradient descent를 돌린다고 가정했을 때, J라는 manifold를 타고 내려가는 그 process를 표시한 거라고 볼 수 있다.

마지막으로 우리가 지금까지 배운 건 'batch' gradient descent라고 할 수 있는데,
m개의 트레이닝 예제들을 모두 한꺼번에 돌려서 J 계산하는 걸 말하고,
다른 gradient descent 방식들은 m개의 예제들 중 subsets을 다뤄서 계산하며
mini-batch gradient descent, Stochastic dradient descent 방식과 같은 게 있다.
전자는 일부의 subsets, 후자는 항상 하나의 data set만을 사용해서 모델의 parameter을 매번 업데이트 해주는 차이가 있다.
'AI > 머신러닝(코세라)' 카테고리의 다른 글
| [ML] #6 신경망(Neural Networks) (0) | 2024.10.15 |
|---|---|
| [ML] #5 정규화(Regularization) (0) | 2024.10.15 |
| [ML] #4 로지스틱 회귀(Logistic Regression) (0) | 2024.10.14 |
| [ML] #3 다변수 선형 회귀(Linear Regression with Multiple Variable) (0) | 2024.09.20 |
| [ML] #1 머신러닝 개론(Introduction to Machine Learning) (0) | 2024.09.19 |



