문제 접근 및 공부 내용, 풀이는 모두 하단 코드에 "주석"으로 포함되어 있으니 참고해주세요.
문제 유형 보기
더보기
이차원리스트
https://dailyalgo.kr/ko/problems/70
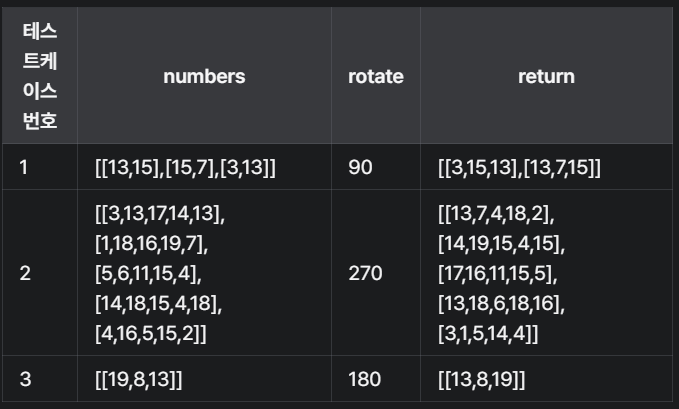
입력 : N x M 자연수로 이루어진 행렬 numbers
그리고 회전할 각도를 나타내는 정수 rotate (= 90 or 180 or 270)
출력 : 회전을 수행한 후의 행렬
1차 풀이(성공)
def solution(numbers, rotate):
N = len(numbers)
M = len(numbers[0])
# N x M matrix numbers
''' 3 x 2
a11 a12
a21 a22
a31 a32
=> 2 x 3
a31 a21 a11
a32 a22 a12
'''
# 열 순회를 아래에서부터 하면 될듯 한데??
# 제일 안에서 j 고정하고 i를 옮겨야 함
# 따라서, J는 바깥에서 돌고, I가 안에서 돌아야 함
if rotate == 90:
return [[numbers[i][j] for i in range(N-1, -1, -1)] for j in range(M)]
''' 3 x 2
a11 a12
a21 a22
a31 a32
=> 2 x 3
a12 a22 a32
a11 a21 a31
'''
# 열 순회를 위에서부터 하되, 마지막 열부터 역순으로 와야함
# 제일 안에서 j 고정하고 i를 옮겨야 하는건 동일
# range가 이번엔 바깥쪽 꺼가 역순으로 돌면 됨.
if rotate == 270:
return [[numbers[i][j] for i in range(N)] for j in range(M-1, -1, -1)]
''' 3 x 2
a11 a12
a21 a22
a31 a32
=> 3 x 2
a32 a31
a22 a21
a12 a11
'''
# 이번엔 행 순회를 하면 되긴 하는데,
# 행과 열 둘다 역순으로 와야함.
# 즉, 둘 다 range가 역순으로 돌면 됨.
if rotate == 180:
return [[numbers[i][j] for j in range(M-1, -1, -1)] for i in range(N-1, -1, -1)]행 순회와 열 순회를 활용한 문제였다.
실전에서 이런 문제를 봤다면, 위처럼 주석으로 빠르게 `간단한 예시`를 관찰해도 좋을 것 같다.
# 리스트 컴프리헨션 안쓴 가장 기본 행 순회 풀이
def solution(numbers, rotate):
N = len(numbers)
M = len(numbers[0])
# N x M matrix numbers
''' 3 x 2
a11 a12
a21 a22
a31 a32
=> 2 x 3
a31 a21 a11
a32 a22 a12
'''
# 열 순회를 아래에서부터 하면 될듯 한데??
# 제일 안에서 j 고정하고 i를 옮겨야 함
# 따라서, J는 바깥에서 돌고, I가 안에서 돌아야 함
if rotate == 90:
rotated_matrix = [[0] * N for _ in range(M)]
for i in range(M):
for j in range(N):
rotated_matrix[i][j] = numbers[N-1-j][i]
return rotated_matrix
''' 3 x 2
a11 a12
a21 a22
a31 a32
=> 2 x 3
a12 a22 a32
a11 a21 a31
'''
# 열 순회를 위에서부터 하되, 마지막 열부터 역순으로 와야함
# 제일 안에서 j 고정하고 i를 옮겨야 하는건 동일
# range가 이번엔 바깥쪽 꺼가 역순으로 돌면 됨.
if rotate == 270:
rotated_matrix = [[0] * N for _ in range(M)]
for i in range(M):
for j in range(N):
rotated_matrix[i][j] = numbers[j][M-1-i]
return rotated_matrix
''' 3 x 2
a11 a12
a21 a22
a31 a32
=> 3 x 2
a32 a31
a22 a21
a12 a11
'''
# 이번엔 행 순회를 하면 되긴 하는데,
# 행과 열 둘다 역순으로 와야함.
# 즉, 둘 다 range가 역순으로 돌면 됨.
if rotate == 180:
rotated_matrix = [[0] * M for _ in range(N)]
for i in range(N):
for j in range(M):
rotated_matrix[i][j] = numbers[N-1-i][M-1-j]
return rotated_matrix# zip을 사용한 풀이
def solution(numbers, rotate):
N = len(numbers)
M = len(numbers[0])
# N x M matrix numbers
''' 3 x 2
a11 a12
a21 a22
a31 a32
=> 2 x 3
a31 a21 a11
a32 a22 a12
'''
# 열 순회를 아래에서부터 하면 될듯 한데??
# 제일 안에서 j 고정하고 i를 옮겨야 함
# 따라서, J는 바깥에서 돌고, I가 안에서 돌아야 함
if rotate == 90:
return list(map(list, zip(*numbers[::-1])))
# 아래처럼 짤 수도 있으나, 위 코드가 좀 더 직관적이므로 일단 위 코드로 기억하자.
# if rotate == 90:
# return [list(row) for row in zip(*numbers[::-1])]
# 이거 고민
''' 3 x 2
a11 a12
a21 a22
a31 a32
=> 2 x 3
a12 a22 a32
a11 a21 a31
'''
# 열 순회를 위에서부터 하되, 마지막 열부터 역순으로 와야함
# 제일 안에서 j 고정하고 i를 옮겨야 하는건 동일
# range가 이번엔 바깥쪽 꺼가 역순으로 돌면 됨.
if rotate == 270:
return list(map(list, list(zip(*numbers))[::-1]))
''' 3 x 2
a11 a12
a21 a22
a31 a32
=> 3 x 2
a32 a31
a22 a21
a12 a11
'''
# 이번엔 행 순회를 하면 되긴 하는데,
# 행과 열 둘다 역순으로 와야함.
# 즉, 둘 다 range가 역순으로 돌면 됨.
if rotate == 180:
rotated_matrix = [[0] * M for _ in range(N)]
for i in range(N):
for j in range(M):
rotated_matrix[i][j] = numbers[N-1-i][M-1-j]
return rotated_matrix# 조건문 분기 안 하고, 90도 회전을 구현한 후, 그걸 여러번 돌리는 걸로 구현하겠다!
# 강사님은 이게 코테에 나왔다면 이렇게 풀었을 거라고 함.
# 이 풀이 선택 가능한 근거 : 시간복잡도 어차피 커야 3배? 될테니 괜찮다.
def solution(numbers, rotate):
''' 3 x 2
a11 a12
a21 a22
a31 a32
=> 2 x 3
a31 a21 a11
a32 a22 a12
'''
for _ in range(rotate//90):
N = len(numbers)
M = len(numbers[0])
# N x M matrix numbers
# 매번 N과 M을 초기화해줘야함!!
rotated_matrix = [[0] * N for _ in range(M)]
# rotated_matrix를 기준으로 행 순회를 돌아야 하니까!!
for i in range(M):
for j in range(N):
rotated_matrix[i][j] = numbers[N-1-j][i]
numbers = rotated_matrix
return rotated_matrix250218 재풀이
def solution(numbers, rotate):
for _ in range(rotate//90):
n = len(numbers)
m = len(numbers[0])
rotated_numbers = [[0] * n for _ in range(m)]
# m x n으로 미리 초기화
for i in range(m):
for j in range(n):
rotated_numbers[i][j] = numbers[n-1-j][i]
numbers = rotated_numbers
return rotated_numbers'Algorithms and Languages > 파이썬 알고리즘 문제풀이' 카테고리의 다른 글
| [Python/백준] 1931. 회의실 배정 (0) | 2025.02.05 |
|---|---|
| [Python/프로그래머스] 42746. 가장 큰 수 (0) | 2025.02.05 |
| [Python/DailyAlgo] 69. 이차원 배열에서 특정 구간 행순회 (0) | 2025.02.05 |
| [Python/백준] 2738. 행렬 덧셈 (0) | 2025.02.05 |
| [Python/DailyAlgo] 79. 배열 정렬 (0) | 2025.02.04 |
