
Digital Image Processing, 4Th Edition: Rafael C. Gonzalez, Richard E. Woods
본 글은 위 교재를 주교재로 한 학교 '영상처리(Image Processing)' 수업을 들으며 공부한 내용을 정리한 글입니다.
해당 글은 개인 공부 및 교육 목적으로 작성하였으며, 일부 교재에 첨부된 사진(또는 교재에서 강의노트로 첨부된 사진)들을 포함하고 있습니다.
교재 출처 사진을 최소화하고자 블로그에는 핵심 사진을 제외하곤 옮기지 않은 사진들도 있습니다. 따라서 고의로 누락한 사진들이 존재하며, 해당 사진들을 언급하는 내용이 있을 수 있습니다. 누락한 사진들은 직접 교재를 참고해 주세요.
혹시 문제가 있다면, 댓글 남겨주시면 빠른 시일 내에 확인 후 적절한 조치를 취하겠습니다.
목차 (Contents)
- 인간의 시각 (Human Vision)
- 빛 (Light)
- 디지털 영상 획득 (Digital Image Acquisition)
- 샘플링, 양자화 및 재샘플링 (Sampling, Quantization, & Resampling)
- 픽셀 간의 기본 관계 (Basic Relationships Between Pixels)
- 수학적 도구 (Mathematical Tools)
- OpenCV 기초 (OpenCV Basics)
인간의 시각 (Human Vision)
안구의 주요 구성 요소 (Optic Components)
- 각막 (Cornea)
- 전안방 (Anterior Chamber)
- 홍채 (Iris)
- 수정체 (Lens)
- 모양체근 (Ciliary Muscle)
- 유리체 (Vitreous Humor)
- 망막 (Retina)
각막 (Cornea)
- 굴절률(Refraction Index)이 높음
- 돋보기 역할을 함
- 굴절 오류 발생 가능 → 근시, 원시, 난시를 유발
- 나이가 들면서 탈색(Decoloration)이 발생하여 색 인식에 영향을 줄 수 있음
홍채 (Iris)
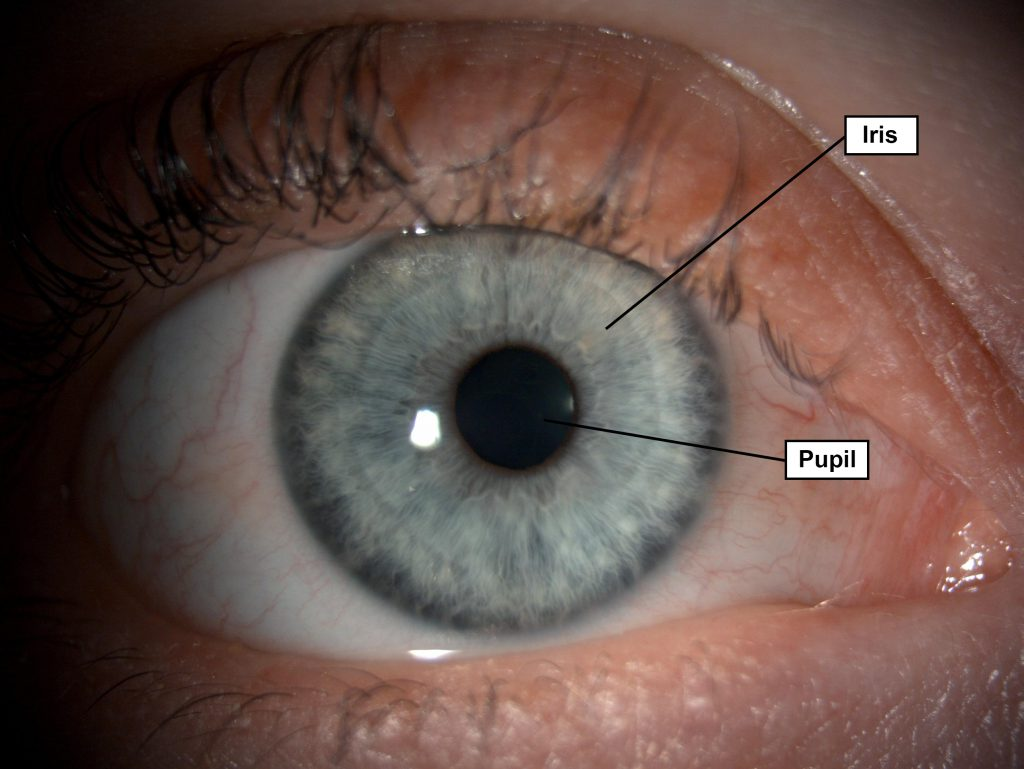
- 원형 구조
- 괄약근(Sphincter Muscle)을 가지고 있음
- 중앙에 동공(Pupil, 구멍)이 존재
- 괄약근은 조여줬다 풀어주는 원형 근육인데, 이걸로 동공 크기를 조절함.
- 조리개(Aperture Stop) 역할을 함.
- 들어오는 빛의 세기를 조절함
- 눈 색깔 결정
- → 멜라닌(Melanin) 농도에 따라 다름
- 멜라닌 색소는 홍채에도 있고 머리카락에도 있고 그럼.
- 단순히 홍채만으로는 인간의 시각이 감지할 수 있는 빛의 세기 범위를 완전히 설명할 수 없음
- 얘는 매우 커져 봤자 100배까지밖에 안 되는데, 사람은 빛의 세기를 10000배까지도 감지할 수 있음.
- 그러니 홍채만으로 우리가 빛의 세기를 조절한다고는 못함.(예전에는 홍채만으로 조절한다고 배웠다고함.)
수정체 (Lens)

- 초점 조절(Accommodation) 기능 수행
- 두꺼워지면 가까운 곳을 초점
- 평평해지면 먼 곳을 초점
- 노화 시: 수정체가 단단해져 유연성을 잃음
- → 통통해지지 못하고 얇아짐
- → 초점이 멀리 잡혀서 가까운 게 안보임
유리체 (Humors)
- 유리체(Vitreous Body)라고도 함
- 수정체와 망막 사이를 채우는 투명한 젤 물질
- 안구의 형태를 유지하며 외부 충격으로부터 보호함
- 주변 압력보다 약간 높은 압력을 유지하여 안구 변형을 방지함(모양을 잡아줌).
- 굴절률이 상대적으로 낮음
Retina(망막)
- 여기까진 참고사항이었고, 이제부터 중요.
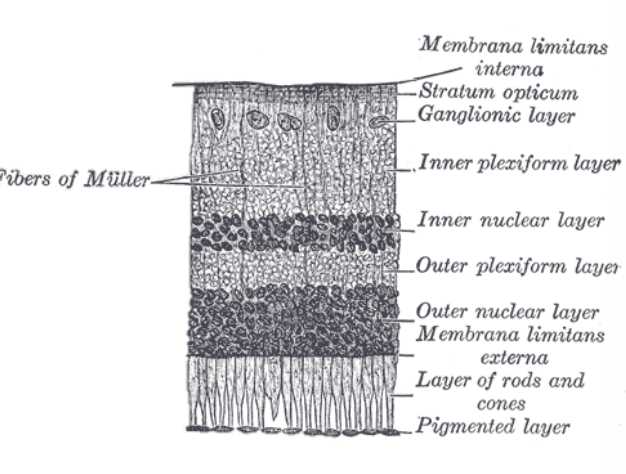
- 위쪽에는 딥러닝처럼 각종 신경들이 들어가 있음.
- 중요한 건 아래쪽에 시세포(Photoreceptors)임.
- 빛을 받으면 신경 자극을 위쪽으로 보내줌.
- 근데, 재밌는 건 센서는 아래쪽에 있는데, 빛은 위에서부터 들어와 아래로 쭉쭉 내려가서 아래쪽에서 센싱됨.
- 그리고 그 센서보다 아래쪽은 엄청 어둡게 되어있어서, 반사가 안되게 만듦. 빛이 아래쪽에서 반사돼서 다시 올라오는 걸 막음.
- 근데, (특히 야행성) 동물들은 저 부분이 반사가 잘 되게 되어있는데, 그건 정밀도는 좀 포기하더라도 최대한 빛을 잘 받아서 밤에도 잘 보려고 그러는 거임.
- 저 시세포를 나중에 뜯어보니까, cone과 rod(뾰족하게 생긴 것과 길다랗게 생긴 거) 두 종류가 있더라~~ 알게 됨.
- 시세포 유형:
- Cones → 명순응(Photopic Vision, 밝은 환경에서 색상 감지)
- Rods → 암순응(Scotopic Vision, 어두운 환경에서 감지)
Rod
- 약한 빛에서 기능을 수행 (야간 시야 담당)
- 망막의 바깥쪽 가장자리에 집중적으로 분포
- 총 개수: 9000만 ~ 1억 2000만 개
- 기능:
- 주변 시야, 야간 시야 제공
- → 이게 망가지면 터널 시야(Tunnel Vision) 형성
- 주변 시야, 야간 시야 제공
Cone
- 색상을 감지하는 역할 수행
- 디테일하게 보는 역할을 수행함. ex. 글씨
- 밝은 환경에서 가장 잘 작동 (Photopic Vision)
- 그래서 어두우면 cone이 아니라 rod만 작동해서 책을 잘 못보는 거임.
- 황반 중심오목(Fovea Centralis)에 집중 분포
- 총 개수: 600만 ~ 700만 개
- 세 가지 유형:
- 장파장(L), 중파장(M), 단파장(S) 감지 → 비율 12:6:1
- 기능:
- 중앙 시야, 주간 시야, 디테일 감지, 색상 감지 제공
Fovea
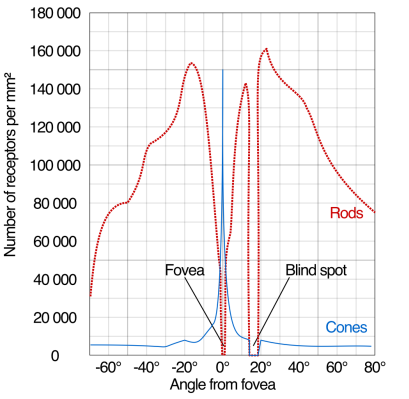
- 저렇게 cones가 가운데에 모여 있어서, 우리는 외곽의 글씨같은건 디테일하게 잘 못봄. 저렇게 cones가 모여있는 곳을 Fovea라고 함.
- 저기 blind spot도 있음 맹점.
Image Formation in the Eye
- 저 C가 초점(optical center)임.
Brightness Adaptation & Discrimination
- 가로가 밝기, 세로가 반응 정도인데,
- 굉장히 어두울 때는 rod가 반응하다가,
- 적당히 밝기가 돌아오면 cone가 반응하기 시작함.
- 중간에 겹치는 부분도 많이 있음.
Brightness Discrimination
- 웨버의 법칙
- 초기의 자극에 따라 자극을 느낄 수 있는 폭이 달라진다.
- 따라서, 어두운 데서 조금 밝아진 건 느껴지는데, 밝은 데서 조금 어두워진 건 안느껴짐.
- 이제부터 재밌는 얘기(사람 눈이 바보같다)
Interesting Properties
- 마크 밴드 이펙트
- 저 사진을 잘 보고 있으면, 같은 칸에서 왼쪽보다 오른쪽이 조금 더 어두워보임. 실제로 우리가 느끼는 밝기는 어두운 건 더 어두워 보이고, 밝은 건 더 밝아 보임.
- 동시대비
- 가운데 있는 사각형의 밝기는 실제론 셋 다 같은데 다르게 보임.
- 눈에서 나가는 곳에 있는 그 뉴럴 네트워크 부분이 잘못된 영향인지, 뇌 영향인지, 아까 베버 효과의 영향인진 아직 모름.
- 등 등…
Interesting Properties: Optical Illusion(착시 현상)
- 안 보여야 될 게 보인다: 사각형이 보임! 원(배경에 비해 가운데가 더 밝게 보이는)이 보인다! 선 길이는 실제로 같다! 저 선들은 다 평행하다!
Interesting Properties: Crispening
- 이거 세로로는 색이 다 같음.
- 근데 저거 가로 색들이 자기랑 비슷한 배경 색에 있을 때 두 차이가 더 크게 느껴짐.
- 배경 색에 따라 차이가 다르게 다가온다.
- 즉, 비슷한 것들 사이에 있을 때는차이가 더 극명해지는 현상.
Interesting Properties: Structural Effect
- 색이 달라보였는데, 선을 그어주고 나니까 같게 보임.
- 보고 있으면 점이 반짝반짝 함.
Neon Color Spreading
- 저기가 하늘색으로 원이 색칠된 것처럼 보임!! 근데 실제론 그냥 선만 칠해진 거임. 오른쪽도 색깔이 그려진 원이 보이나 선만 칠해진 거임.
Watercolor Illusion
- 저것도 다 하얀색인데 중간에 노란색이 보이기 시작함.
- 이것도 색이 (같은가?)한데, 초록 빨강으로 보임.
Lights
Human Vision
- 빛 얘기를 좀 해야겠다.
What’s Happening?
- 빛이 광원에서 나와서, 세상을 돌아다니면서 감쇄가 됨.
- 그러다 물체를 만나면, 물체는
- 이 빛을 일부는 흡수(에너지 흡수해서 없앰),
- 일부는 반사(에너지 일부 잃어버리지만 거울처럼 거의 다 반사해냄),
- 일부는 스캐터링함(에너지를 사방으로 퍼뜨림.)
- 그러다 사람 눈으로 들어오면 시세포가 반응해서 보게 되는 거임.
Newton Experiment
- 뉴턴의 프리즘 실햄 → 빛은 복잡한 색이 섞여 있다는 가설을 세움.
Electromagnetic Spectrum
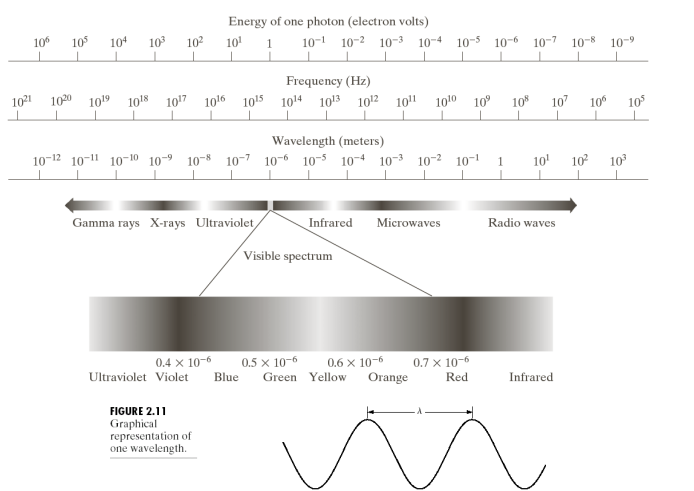
- 빛은 전자기파 중에서 사람의 눈으로 감지 가능한 가시광선 영역의 전자기파를 일상적으로 부르는 말임.
- 왼쪽으로 갈수록 파장이 짧아지고, 오른쪽으로 갈 수록 파장이 길어짐.
Light
- 전자기파 중 사람이 봤을 때 보이는 것만 빛이라고 함. → 가시광선 영역.
- 다른 에너지 비율을 가지고 모여서 만든 결과는 에너지인데, 이 에너지를 사람이 보고 ‘빨간색!’이라고 느끼면 색깔이 됨.
- monochromatic light라고 흑백으로 밝기만 따지기도 하는데, 우리는 당분한 밝기만 따져서 회색으로 접근할 거임..
Image Acquisition
Sensor Elements
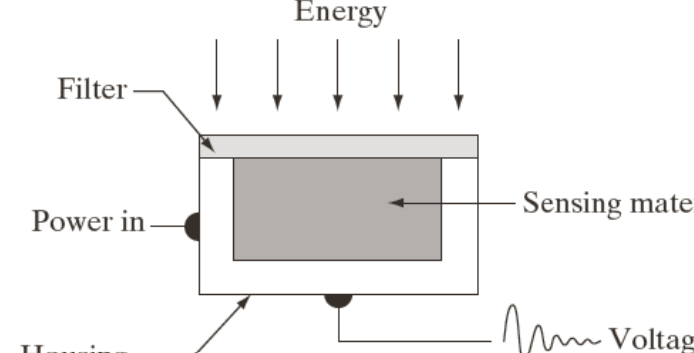
- 저 빛의 세기를 측정해줄 수 있는 놈이 필요함 → 센서.
Typical Sensing Devices
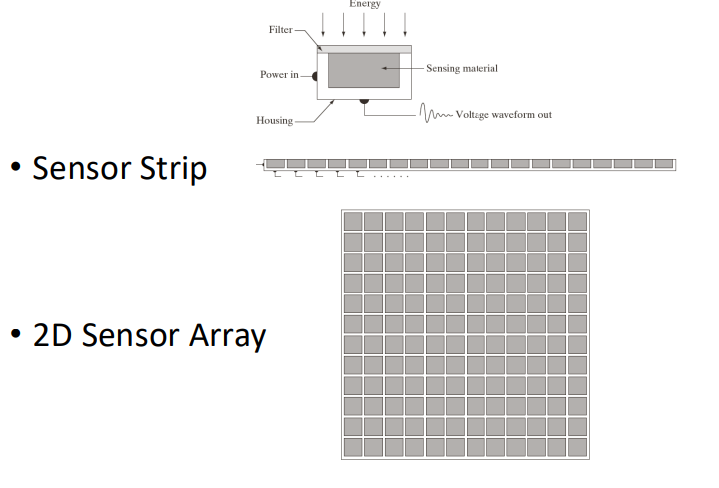
- 센서를 한 줄로 붙여둬서 세로로만 움직이는 걸 sensor strip이라 함.
- 센서를 2차원 행렬 형태로 배열하면 2D sensor array임.
Single Element Sensing
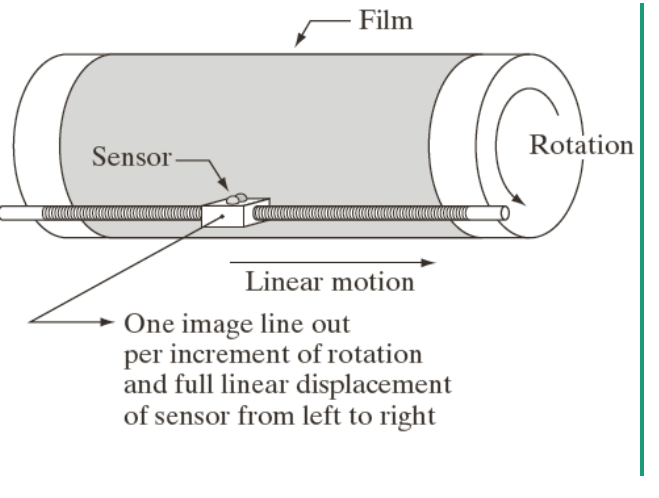
- 예를 들어서, 종이를 스캔하고 싶은데센서가 하나밖에 없으면? → 한 줄 한쪽방향으로 쭉 하고 쪼끔 내려가서 쭉 하고~~
- ex. (센싱은 아니지만)잉크젯 프린터.
- 잉크젯 프린터의 헤드는 소모품이라 이게 막히거나 고장나면 교체하고 해야 하는데, 이걸 sensor strip으로 쓰면 비용이 많이 듦.
- 근데, 센서가 한 줄로(sensor strip) 있으면, 그냥 한 줄로 쭉 내려가면 됨. ex. 스캐너, 엑스레이
- 둘 중 어느게 더 비쌀까?
- 옛날에는 센서가 한 줄로 쫙 있는 게 더 비쌌음.
- 근데 요즘은 센서 가격이 더 싸져서, 저걸 좌우로 움직이는 장치가 더 비싸져서, 센서 하나로 쓰는 게 더 비쌈.
- 저 하나짜리 센서 쓰는 거 장단점
- 단점: 겁내 오래걸림.
- 장점: 저걸 한 줄 스캔할 때 천천히 움직히면, sampling을 더 촘촘히 해서, 더 디테일한 사진을 얻을 수 있다 → 즉, 가로 해상도를 더 높게 가져갈 수 있다.
- 근데, 이와 반대로 한 줄짜리 놈은 가로 해상도는 이미 정해져 나온 거임. 세로 해상도는 바꿀 수 있지만. 그래서 스캐너 살 때 가로 해상도 봐야 한다.
2D Image Array Sensing
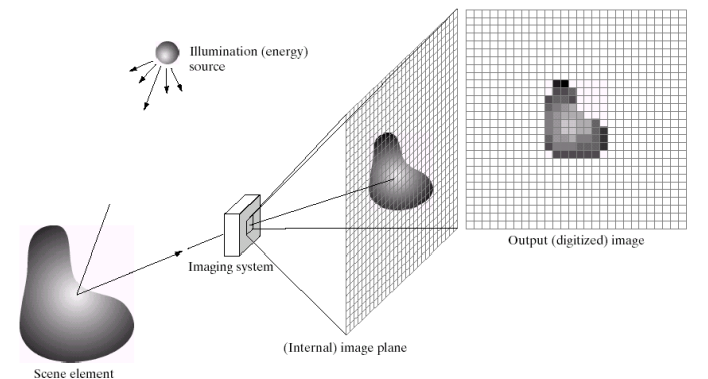
- 요즘은 다 저런 식으로 센서를 배치함. ex. 카메라
- 장단점:
- 중요한 장점은 한 번만에 센싱이 가능하단 거고,
- 단점은 구성 시 해상도가 정해져버린다는 것임.
- 그래서 애플이랑 삼성이 이걸로 싸웠었음. 우리는 몇 픽셀(화소)이 들어갔다~~
Typical 2D Sensor Array
카메라 센서 만드는 기법인데 요즘은 저렇게 안 만들고, CMOS로 만듦.
Image Formation Model
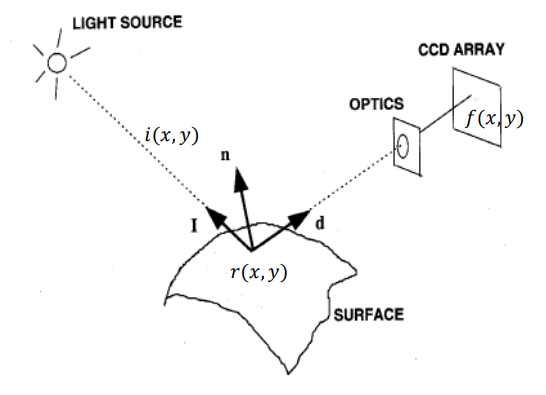
- 빛이 광원에서 와서 반사가 돼서 센서로 들어오는데, 그 때 밝기는 도대체 어떻게 되냐??
0 < 𝑓(𝑥, 𝑦) < ∞: 광원에서 오는 빛의 세기(조명)(Illumination)는 우리가 제한을 못함. 따라서 0~무한대.0 < 𝑖(𝑥, 𝑦) < ∞로 표시하기도 함.
- 얘가 반사가 될 때 r이라는 값이 곱해져서 오지 않을까? 하고 생각하는 거
0 < 𝑟(𝑥, 𝑦) < 1은 반사율(Reflectance)이라고 부르는데, 들어온 빛을 얼마나 반사했냐 그 비율임. 이건 스캐터율 이런 것도 통합한 개념임.- 사실 굳이 따지면 저 r은 스캐터율로 부르는 게 맞긴 함.
- 반사는 온 대로 수직방향으로 반사돼야 하는 거고,
- 지금은 빛이 들어가서 쪼물딱거리다가 빛을 흩뿌리는 거임.
- 일단, 저 반사하는 놈(surface)는 자기가 빛을 받는다고 에너지를 새로 만들진 않음.(형광, 야광 같은 놈들 제외)
- 그래서 반사율은 0~1정도로 생각하는데, 아직 0인 놈이나 1인 놈이 없어서 등호는 안 넣음.
Reflectance Examples
- 검은색 벨벳(Black Velvet) → 0.01
- 스테인리스 스틸(Stainless Steel) → 0.65
- 흰색 벽 페인트(Flat-White Wall Paint) → 0.80
- 은도금된 금속(Silver-Plated Metal) → 0.90
- 눈(Snow) → 0.93
- 최근엔 반타블랙이 0.045%로 반사율 가장 낮고, 황산 바륨은 반사율이 잘만 하면 0.98%까지 감.
Intensity Range
- (우리는 지금 흑백만 보고 있음, 즉 픽셀에 대한 값(깊이값)을 밝기값 하나만 가짐.)
- 픽셀의 밝기를
l = f(x, y)라고 나타낼 건데, (x, y)위치의 밝기가 l이라는 소리임. - 밝기 범위를
L_min <= l <= L_max로 정의하는데, - 보통은 L_min을 0, M_max를 L - 1로 둠.
0→ 검정(Black)L - 1→ 흰색(White)L - 1보다 더 밝은 게 들어오면 → 포화(Saturation, 너무 밝아서 정보 손실)- 이 경우 센서의 한계로
L - 1값이 센싱됨.
- 이 경우 센서의 한계로
- 범위를 최대값과 최소값 사이에 있다고 생각한단 거임. 그래서 우리는 이걸 0을 검은색으로 보고, 0~L-1사이를 빛의 세기로 볼 거임. L-1(제일 밝은 색)은 하얀색이다.
- 근데, 센서의 최대치가 L-1인데 L-1보다 더 밝은 게 들어오면 그냥 L-1로 재버림. 이런 상황을 saturated(포화)됐다고 함.
샘플링과 양자화(Sampling and Quantization)
기본 개념 (Basic Concept)
- 샘플링(Sampling):
- 연속적인 이미지를 픽셀 단위로 나누어 저장. 해상도가 높을수록 샘플링 횟수가 많음.
- 예: 1920×1080 해상도의 이미지는 가로 1920개, 세로 1080개의 픽셀로 이루어짐.
- 여기서 각 픽셀들은 그 픽셀의 대푯값을 픽셀 값으로 가짐. 뭐 평균을 내든 중앙부분을 갖든 함. 근데 이 픽셀 값은 실수 범위.
- 연속적인 이미지를 픽셀 단위로 나누어 저장. 해상도가 높을수록 샘플링 횟수가 많음.
- 양자화(Quantization):
- 각 픽셀의 색상 값을 8비트(0~255) 또는 16비트 등으로 근사하여 저장.
- 예: 흑백 이미지는 0(검은색)에서 255(흰색) 사이의 값으로 표현됨.
- 컬러 이미지는 RGB 각각 8비트(0~255)로 양자화되어 16,777,216가지 색상을 표현함.
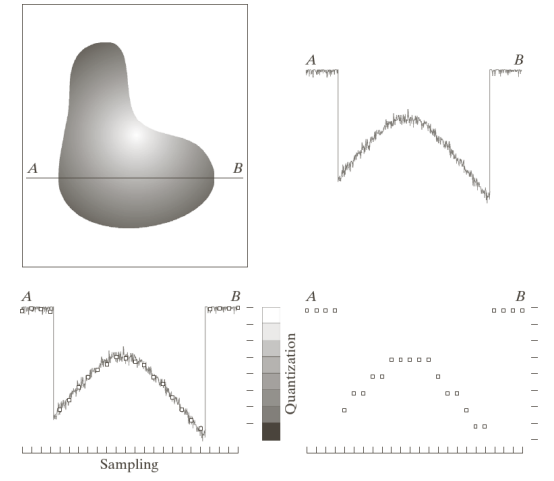
- 각 픽셀의 색상 값을 8비트(0~255) 또는 16비트 등으로 근사하여 저장.
- 저기 저 AB 사이 그은 한 선을
scan line이라고 관습적으로 부름. - 위에 오른쪽은 밝기 그래프.
- 근데 저걸 다 표현할 수 없으니, 구간마다(즉, 픽셀 단위로) 일정한 대표값으로 변환함. 여기까지 샘플링.
- 즉, x, y값으로 표현되는 연속적인 이미지를, 일련의 픽셀이라는 값들가지고 그 이미지를 표현하겠다는 거임. 이 과정에서 각 픽셀을 특정 값으로 대표하게 됨.
- 근데 그걸 가지고 한정된 정밀도의 정수 값들로 대응하는 게 양자화.
- 흑백 이미지를 예시로 들면, 0, 1, …, 255 중에서 가장 가까운 놈으로 대응시키는 거임.
- 근데 저걸 다 표현할 수 없으니, 구간마다(즉, 픽셀 단위로) 일정한 대표값으로 변환함. 여기까지 샘플링.
- 양자화에서 픽셀 개수가 변하는 게 아님. 오해x.
Sampling
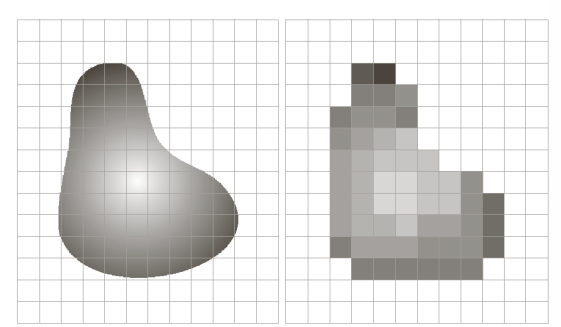
- 수학적으로 보면:
- 샘플링 및 양자화를 하고 나면, 도메인(정의역)이 2차원 실수 공간(R^2)에서 2차원 자연수 공간(N^2)으로 바뀜.
- 하드웨어적으로 보면:
- 2D 센서 배열에서 샘플링이 진행됨.
- (아님 센서 스트립으로 쭉 훑으면서 진행하거나)
Representation Digital Images
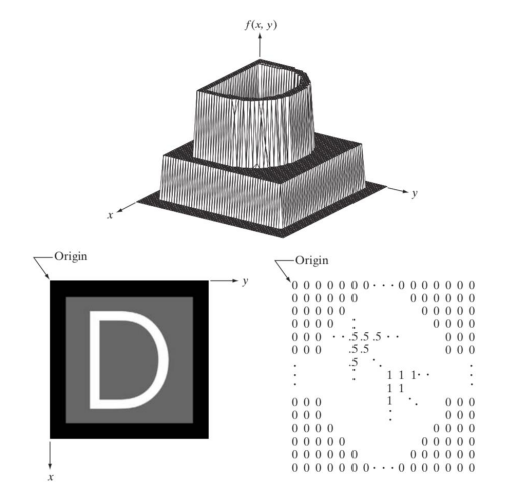
- 저렇게 각각의 칸에 숫자값을 대응해 이미지를 나타낼 수 있음 → 이걸 raster(bitmap) image라고 부른다고 저번에 했다!!


- 저렇게 이미지를 MxN 행렬의 형태로 저장할 수 있겠다!(실제로 프로그래밍할 때도 이미지를 행렬로 다룰 것임.)
Quantization
- 한 픽셀 당 k개의 비트를 쓸 경우, 한 픽셀이 가질 수 있는 정수값은 2^k개가 됨.
- L = 2^k라고 할 때, 픽셀이 가질 수 있는 값은
[0, 𝐿 − 1]자연수.
- L = 2^k라고 할 때, 픽셀이 가질 수 있는 값은
- 즉, M x N 이미지는 한 픽셀 당 k개의 비트를 쓸 경우 해당 이미지를 저장하는 데
𝑏 = 𝑀 × 𝑁 × k개의 비트가 필요함.- 보면, 그래서 용량이 상당히 커질 수도 있음. 그래서 압축이 필요.
- 예를 들어, 6000 x 4000 픽셀의 2400만 화소 카메라가 비트 깊이 24비트(RGB 각각 8비트)로 사진을 찍으면, 약 576MB가 필요함. (1MB = 1,000KB = 1,000,000B로 계산)
Saturation & Noise
- 저게 우리가 디지털로 변환해 저장할 때는 최소값 최대값이 존재하기에, 저 부분이 디지털로는 같은 최대 밝기로 나오지만, 실제론 더 밝아졌다 어두워지고 있을 거임.
Spatial and Intensity Resolution
- 공간 해상도 (Spatial Resolution)
- 얼마나 작은 공간까지 구별 가능하게 표현할 수 있는가?
- Stated with line pairs per unit distance
- dots (pixels) per unit distance
- dots per inch(dpi)
- 얼마나 작은 공간까지 구별 가능하게 표현할 수 있는가?
- 세기 해상도 (Intensity Resolution)
- 얼마나 작은 밝기 변화까지 구별 가능하게 표현할 수 있는가?
- 즉, 픽셀 깊이라고 보면 됨.
- 강도 해상도는 이미지에서 밝기(또는 색상)의 변화를 얼마나 세밀하게 표현할 수 있는지를 의미함. 즉, 두 개의 서로 다른 밝기 값을 사람이 또는 센서가 구분할 수 있는 정도를 나타냄.
- 이것은 비트(bit) 단위로 표현되며, 일반적으로 다음과 같은 방식으로 사용됨:
- 8비트(256 단계): 0(검은색)부터 255(흰색)까지의 밝기 수준을 표현 가능.
- 12비트(4,096 단계): 더 정밀한 밝기 표현 가능.
- 16비트(65,536 단계): 매우 높은 수준의 밝기 변화를 구별할 수 있음.
- 얼마나 작은 밝기 변화까지 구별 가능하게 표현할 수 있는가?
공간 해상도 vs 세기 해상도(비트 깊이)
- 공간 해상도가 높은 게 나을까, 세기 해상도(비트 깊이)가 높은 게 나을까?
- 뭐 사람이 많으면 공간 해상도가 중요하고, 얼굴 하나면 세기 해상도가 중요해진다 이런 말이라는데 별로 안중요한 내용이라 함.
Image Interpolation(이미지 보간)
- 보간법(Interpolation)이란?
- 알려진 데이터를 이용해 모르는 값을 추정하는 방법
- 이미지 보간(Image Interpolation)
- 픽셀 간의 값을 예측하여 이미지의 해상도를 높임
- 수학적으로는:
f(i, j)라는 픽셀값을 가지고v(x, y)라는 픽셀값을 만들어냄.
- 내가 이미지를 크게 만들고 싶어서 새로운 이미지를 만들고 싶을 때, 내가 원하는 픽셀과 1대1 대응이 안될 수 있잖음?(저 시계처럼) 그러면, 거기 픽셀 값을 정수로 가져오고 싶은데, 실수로 가져와야 하는 일이 생김.
- 그니까, 예를 들어, 3배 확대했으면, 같은 픽셀 크기가 되려면 원래꺼 한 칸 기준 0.333…인 위치에서 픽셀을 내가 가져와서, 새 사진의 한 칸에 박아넣어야 하는데, 0.333을 어떻게 읽겠냐는 거임.
- 또는, 일단 키워놓은 다음에 그럼 사이사이에 픽셀들을 채워넣으려고 하는데, 어떻게 채워넣겠냐는 거임.
- → 그러면 그거 주변 4개 픽셀 값을 어떻게 짬뽕해주면 되지 않을까?
- 각 픽셀의 값을 그냥 그 픽셀의 가운데에 점을 찍어서 그 값을 나타낸다고 생각해보자.
Typical Interpolation
최근접 이웃 보간법 (Nearest Neighbor Interpolation)
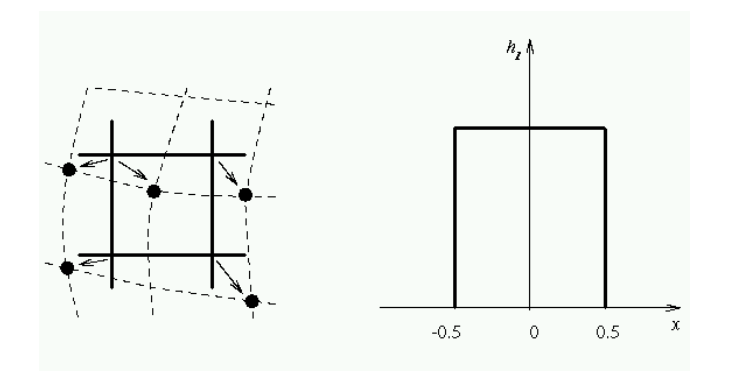
- 가장 가까운 픽셀 값을 그대로 사용
- 수식:
v(x, y) = f(round(x), round(y))
- 특징:
- 빠르지만 이미지가 거칠어질 수 있음
- 저 격자들에서 점으로 값을 가져오겠다.
양선형 보간법 (Bilinear Interpolation)
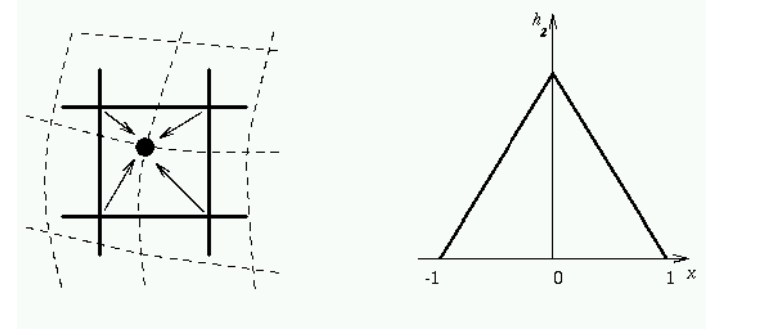
- 주변 4개 픽셀 값을 사용해 보간
- 수식:
v(x, y) = ax + by + cxy + d
- 특징:
- 부드러운 결과를 제공하지만 약간의 흐림 발생 가능
- 얘는, 아까 그 1 2 3 4 점이 있을 때, 누가 얼만큼 새 픽셀값에 기여할까? 하는 거. 해당 점들에 더 가까울수록 기여치가 더 높아짐. 그걸 그래프로 그려보면 오른쪽처럼 거리에 따라 증가하고 감소하는 그래프가 나옴. 결국, x와 y에 대한 1차식으로 나옴. 두 방향(bilinear) 보간. 세 방향이면 tri~ 해서 입체가 됨
- 계수 4개가 필요함.
양삼차 보간법 (Bicubic Interpolation)
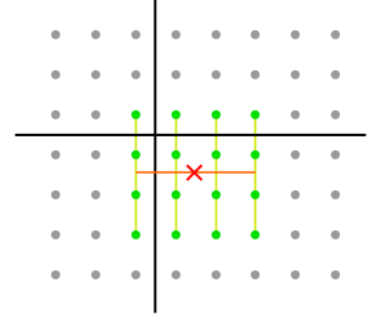
- 주변 16개 픽셀 값을 사용하여 보간
- 수식:

- 특징:
- 가장 부드러운 이미지 생성 (고화질 확대 시 유용)
- 근데 얘는, 아까는 좀 1차식으로 직선의 형태로 보간을 했지만, 얘는 이제 그 보간이 곡선의 그래프 형태가 아닐까 하고 추측하는 거임.
- 부드러운 곡선 그래프를 만드려면, 아까 1차와 달리 이젠 차수를 높여줘야 함. 여기선 3차식(cubic)으로 만들었음.
- 여기선 아까 계수 4개와 달리, 계수 16개가 필요함. 즉, 얘는 자기 주변에 16개의 픽셀 값을 봐야함. (2차로 안한 건, 2차로 하면 어디까지 봐야 할 지 애매해짐. 3개 3개 하면 좀 애매.)
Image Interpolation
- 그 결과는, 위 시계 그림과 같음.
- 각각을 세 가지 보간법을 사용해, 화질이 떨어진(또는 확대한) 시계 사진의 해상도를 높인 것.
- 딱 봐도 맨 마지막에 Bicubic Interpolation이 젤 보간 성능이 좋음.
- 근데, cubic은 경우의 수에 따라 부드럽게 가려다 보니 더 아래나 더 위로 값이 overshooting할 수 있음. 원래 없던 게 생김.(U자 그래프, S자 3차 그래프)
- 근데 그럼에도 불구하고 linear보단 좋다.
Basic Relationship between Pixels
Neighborhood
- 이웃이다(Neighbors)
- 4-이웃이다(4-neighbors) - N_4(p)
- 자기 주변 상하좌우 놈들이 4-이웃임.
- 4-대각이웃이다(4-diagonal neighbors) - N_D(p)
- 자기 주변 대각4방향 놈들이 4-대각이웃임.
- 8-이웃이다(8-neighbors) - N_8(p)
- 자기 주변 8방향 놈들이 8-이웃임.
- 4-이웃이다(4-neighbors) - N_4(p)
Adjacency
- 인접하다(Adjacency)
- 4-인접하다(4-adjacency) - q ∈ N_4(p)
- 두 픽셀이 4-이웃 관계이다.
- 8-인접하다(8-adjacency) - q ∈ N_8(p)
- 두 픽셀이 8-이웃 관계이다.
- M-인접하다(M-adjacency)
- 두 픽셀이 다음 조건 중 하나라도 만족한다면, 두 픽셀은 M-인접한다.
- q ∈ N_4(p) 또는
- q ∈ N_D(p) 이며 N_4(p) ∩ N_4(q) 가 공집합일 때
- 두 픽셀이 다음 조건 중 하나라도 만족한다면, 두 픽셀은 M-인접한다.
- 4-인접하다(4-adjacency) - q ∈ N_4(p)
- 8-인접과 M-인접의 차이??
-
0 0 0 0 p 0 q 0 0 0 0 0 0 p 0 q 1 0 - https://stackoverflow.com/a/45344426
- M-인접은 8-인접의 특수한 경우.
- 위 1번 예시의 p와 q는 8-인접하며 M-인접하지만,
- 위 2번 예시의 p와 q는 서로의 4-이웃의 교집합이 공집합이 아니기에, 8-인접하나 M-인접하지 않음.
-
Path (or Curve)
- 자기랑 같은 속성을 같고 있는 픽셀들의 집합 중에서,
- 인접한 놈들을 이으면 경로가 나온다.
- 자기 자리로 돌아오면 닫힌 경로.
- 자료구조 시간에 배운 Path와 정의가 동일함.
- (x0, y0) = (xn, yn)일 때는 Closed Path가 됨.
- 4-경로, 8-경로, M-경로가 존재함.
8-and m-path

- 위 예시에서, 왼쪽 꺼는 8-경로이자 m-경로이나,
- 오른쪽 꺼는 8-경로이지만 m-경로는 아님.
- (0, 2)와 (1, 1)위치 두 픽셀이 교집합 (0, 1)을 가져 m-경로가 아니기 때문이다.
Connected
- 두 픽셀 사이에 경로가 존재하면 연결되어있다고 한다.
- 4-연결, 8-연결 등이 정의됨.
- 연결 요소: 연결된 서브그래프 덩어리들.
Region(지역)
- 연결된 픽셀들의 서브셋이자, 자료구조 시간에 배운 연결 요소임.
- 인접 지역(Adjacent regions): 연결된 두 지역.
- VS. 서로소 지역(Disjoint regions): 연결되지 않은 두 지역.
- 이러한 지역은 내가 정의하기 나름임.
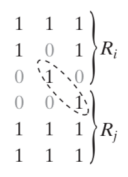
Boundary(경계)

- border 또는 contour라고도 불림.
- Pixels in region R and adjacent to R^c
- 사용할 연결성을 정의해 줘야함.
- 예를 들어, 왼쪽 예시에서 동그라미 친 1은 4-연결성을 사용할 시에는 border이 아님.
- 내부 경계(Inner border)
- 경계 바로 안쪽에 인접해 있는 픽셀들의 집합임.
- 외부 경계(Outer border)
- 경계 바로 바깥쪽에 인접해 있는 픽셀들의 집합임.
0 0 0 0 0
0 1 1 1 0
0 1 1 1 0
0 1 1 1 0
0 0 0 0 0
O O O O O
O B B B O
O B 1 B O
O B B B O
O O O O O- 원본 이미지가 위와 같을 때,
- B가 경계, O가 외부 경계, I가 내부 경계임.
Distance Measure
- 거리가 메트릭이 될 수 있는 조건 3가지(또는 메트릭의 성질 3가지)
- D(p,q)≥0 (D(p,q)=0 "iff" p=q),
- D(p, q)=D(q, p), and
- D(p, z)≤D(p, q)+D(q, z)
- 뻔한 이야기임.
- 흔한 메트릭들
- D_e (p,q)=[(x-s)^2+(y-t)^2 ]^(1/2): Euclidean distance
- D_4 (p,q)=|x-s|+|y-t|: D4 distance (aka city-block distance, Manhattan distance)
- D_8 (p,q)=max(|x-s|,|y-t|): chess board distance
- 인지입이랑 데이터마이닝 수업 때 다 배운 것들.
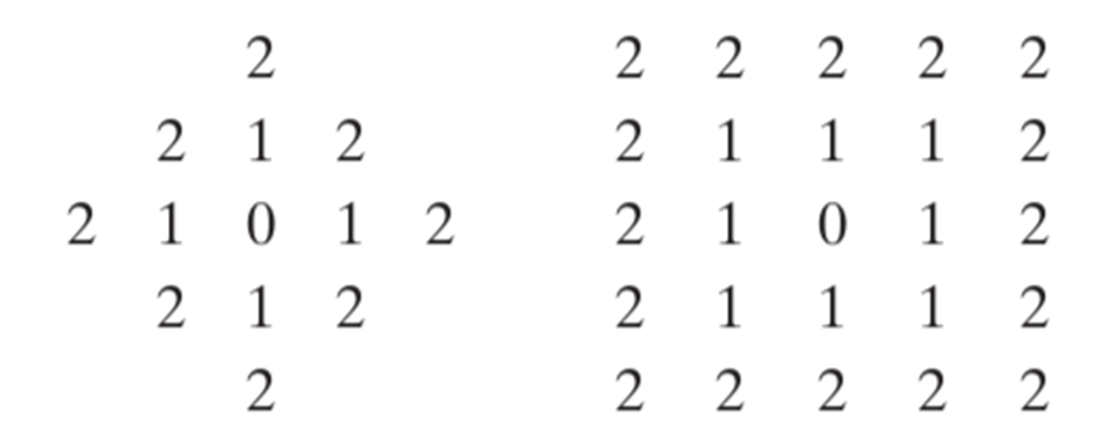
- 가운데 0 기준으로 거리를 표시해보면 위와 같음.
Mathematical Tools Basic
- 수학적인 거 이제 알아보자.
Array vs Matrix Operation
- 기본적인 선대 내용 복습.
Linear vs Nonlinear Operations
- (x, y)가 정수 튜플이면 디지털 이미지라고 부름.
- H[f(x,y)]=g(x,y)
- H라는 오퍼레이션을 한 번 해서, g라는 최종 결과를 내보냈단 뜻임.
- f는 지금은 (x, y) 점(픽셀)의 밝기를 의미.
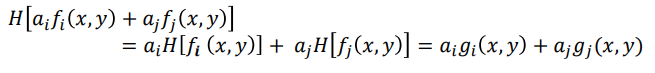
- 위 조건이 성립되면 저 함수(또는 오퍼레이션, 작업) H를 선형적이라고 함.
Arithmetic Operation
- 우리는 원본 이미지에 특정 이미지를 더하거나, 빼거나, 곱하거나, 나눠볼 수 있음
- 임의로 노이즈를 더해줄 수도 있고,
- 이번엔 이미지에서 이미지를 빼 봤더니, 원래 이미지에서 잘 안 보이던 정보가 보이기 시작하기도 한다.
- 이번엔 원소곱인데, 이건 행렬끼리의 곱셈이 아니라 픽셀까지의, 즉 원소곱임.
- 문제가 있는 부분만 1을 곱하고 나머진 0을 곱해, 특정 부분만 볼 수가 있다.
- 이번엔 원소나눗셈인데, 아래쪽으로 갈 수록 밝기가 어두워지고 있어서,
- 이거 밝기를 좀 even하게 만들고 싶었던 거임.
- 그래서 normalization을 해줬다고 봐도 될듯.
Logical Operations
- 전체집합 합집합 교집합 여집합 차집합 개념(당연한 거)
- 위는 교집합 개념 엑스레이 사진.
Pixel-wise Logical Operations
- 여집합, 합집합 개념
OpenCV Basic
- 오픈소스 라이브러리.
- BSD 라이센스임. 아무렇게나 하세요~~ 라이브러리.
- C++, 파이썬, 자바 등으로 사용 가능한데, 자바는 쓰지 마라. 별로임.
- 영상 처리와 컴퓨터 비젼에 쓰임.
Basic Usage
#include <opencv2/core.hpp>
#include <opencv2/highgui.hpp>
using namespace cv;
…
Mat src = imread(“/…./image.png”);
//Converting to float
Mat src32;
src.convertTo(src32, CV_32F, 1/255.f);
Mat pp;
pow( src32, 2.2, pp );
Imshow(“Output”, pp);
waitKey();- 이거 vscode로 직접 실행 가능한 폴더세팅 해두기.
'AI & Data > 컴퓨터 비전(CV)' 카테고리의 다른 글
| [영상처리] Ch3.2. Spatial Filtering (0) | 2025.04.07 |
|---|---|
| [영상처리] Ch3.1. Intensity Transformations (0) | 2025.04.07 |
| [영상처리] Ch1. Introduction. (0) | 2025.03.10 |


