
Digital Image Processing, 4Th Edition: Rafael C. Gonzalez, Richard E. Woods
본 글은 위 교재를 주교재로 한 학교 '영상처리(Image Processing)' 수업을 들으며 공부한 내용을 정리한 글입니다.
해당 글은 개인 공부 및 교육 목적으로 작성하였으며, 일부 교재에 첨부된 사진(또는 교재에서 강의노트로 첨부된 사진)들을 포함하고 있습니다.
교재 출처 사진을 최소화하고자 블로그에는 핵심 사진을 제외하곤 옮기지 않은 사진들도 있습니다. 따라서 고의로 누락한 사진들이 존재하며, 해당 사진들을 언급하는 내용이 있을 수 있습니다. 누락한 사진들은 직접 교재를 참고해 주세요.
혹시 문제가 있다면, 댓글 남겨주시면 빠른 시일 내에 확인 후 적절한 조치를 취하겠습니다.
Contents
- Basics of Intensity Transformations and Spatial Filtering
- Basic Intensity Transformation Functions
- Histogram Processing
Basics of Intensity Transformations and Spatial Filtering
- Intensity Transformation: 밝기를 입력으로 받아서 밝기를 출력으로 내보내는 함수.
- Intensity: 밝기, 세기, 강도 등. 우리는 ‘밝기’로 읽을 것임.
- Spatial Filtering: 공간 필터링
- Spatial: 픽셀 계산을 할 때, 주변에 있는 놈도 끌고와야 할텐데, 이 ‘주변에 있는 놈’을 어떻게 정의할 거냐? → 공간적으로 가까운 픽셀값들. 이게 ‘Spatial’의 개념임
- Filtering: 이미지에서 원하는 정보를 강조하거나, 불필요한 정보를 제거하는 과정.
- 특정 규칙(필터)을 이용해서 픽셀값들을 새로 계산하는 거임.
- 블러(흐림), 샤프닝(선명화), 엣지 검출(윤곽선 찾기) 등이 있음.
- Spatial Filtering: 주변의 픽셀값들을 끌고 와서 필터링을 하는 것.
Intensity Transformations & Spatial Domain

g(x,y)=T[f(x,y)]- (x, y): 2차원 공간상의 좌표.
- 이미지를 표현할 때, 좌표 (x, y)를 넣으면 밝기(Intensity)를 출력하는 함수로 표현함. 여기선
f(x, y)가 이미지.- 이미지는 각 좌표 (𝑥,𝑦)에서 픽셀 밝기(Intensity) 값이 정의된 함수임.
f(x,y)=해당 좌표에서의 밝기 값.
T는 Spatial domain Operator임.- → T는 좌표 (x, y)와 그 이웃들의 픽셀값을 가지고, 그 좌표의 픽셀값을 정의한다는 뜻.
- T는 "이미지에 적용하는 변환(Transformation)"을 의미하는 일반적인 연산자(Operator) 내지 함수임.
Spatial Domain Operator Example
- 그 점과 주변 점들의 밝기 값의 평균을 구하는 함수를 g로 정의할수도 있음.
- 이 때 T를 Average Filter라고 부름. (T가 필터임!! g가 필터가 아님에 주의!!!)
- 4-이웃 필터:
𝑔(𝑥,𝑦)=(1/5)*(𝑓(𝑥,𝑦)+𝑓(𝑥−1,𝑦)+𝑓(𝑥+1,𝑦)+𝑓(𝑥,𝑦−1)+𝑓(𝑥,𝑦+1)) - 8-이웃 필터:
g(x,y)=(1/9)*[∑_(i=-1)^1~1][∑_(j=-1)^1~1][f(x+i,y+j)
- 4-이웃 필터:
- (x, y)를 가운데로 하는 3x3 window를 위치시켜서, 거기에 있는 값들을 가지고 결과를 구함.
Filtering?
- Spatial Filter(공간 필터)
- 계수들의 집합임. (앞에 예시의 1/4나 1/9처럼).
- Image Window에 곱해짐.
- 참고로. 여기서 말하는 ‘곱하기’는, 행렬곱이 아닌 ‘합성곱(컨볼루젼)’임.
- Spatial mask, kernel, template, window 등으로 불림.
합성곱(Convolution)이란?

- 이미지에 필터(커널)를 적용해 이미지의 각 픽셀을 변환하는 작업.
- 작동 과정:
- 커널을 이미지의 각 픽셀에 맞게 이동시켜 가며 계산함.
- 각 이미지의 픽셀 값과 커널의 해당 위치 값을 곱하고 더한 결과를 새로운 픽셀 값으로 사용함.
- 이를 통해 이미지의 특정 특성(엣지, 블러, 샤프닝 등)을 강조할 수 있음.


- 예를 들어, 위와 같은 3x3 평균 필터(우리 강노에서는 8-이웃 필터) h와, 3x3 입력 이미지 f가 있을 때,
- 저걸 그냥 필터링 돌리면 출력 이미지가 1x1로 축소됨.
- 따라서, 보통은 padding을 추가하는데, 0을 padding하는 걸 zero padding이라고 부름.


- 그래서 위처럼 제로 패딩을 추가한 f_padded를 h로 필터링하면, 결과 이미지 g가 나옴.
- 보면 평균으로 얼추 블러 처리가 된 걸 볼 수 있음.
- 참고로, 보면 경계 픽셀값들이 되게 낮아졌는데(즉, 어두워졌는데)
- 이런 제로 패딩의 현상이자 단점을 ‘검은 경계’라고 부름.
Basic Intensity Transformation Functions
- 기본적으로, 어두운 건 어둡게, 밝은 건 밝게 나오는 게 좋잖음.
- 그럼 얼만큼 어둡게, 얼만큼 밝게 해줄까?
- 그리고 밝은 것중에 좀 더 밝은 걸, 얼만큼 좀 더 밝게 해줘야 할까?
Intensity Transformation Functions
- 1-이웃(이란 말은 없지만)의 픽셀만을 가지고 픽셀값을 계산한다면 어떨까??
- 이러면, T는 자기 자신의 밝기만을 입력으로 받아, 밝기를 출력하는 함수가 될 것임.
s=T(r)- f와 g를 이미지라고 할 때, f의 픽셀에 함수 T를 씌웠더니 나온 결과값 s를 g에 쓰겠다!
- 즉, T는 오직 입력 밝기 r을 받아 변환된 밝기 s를 출력하는 함수임.
- 이 때 그 변환 함수 T를 밝기 변환 함수(Intensity Transformation Function)이라고 부름. 또는 그레이-레벨 함수나, 매핑 함수라고도 부름.

- r에 대한 T의 그래프.
- 보면, 자기 자신의 픽셀값만을 가지고 픽셀값을 도출하지 때문에,
- 위처럼 입력밝기 r과 출력밝기 s에 대한 그래프 형태로 표현할 수 있는 거임.
- 왼쪽 그래프의 경우, k부분의 기울기(미분값)이 굉장히 큼.
- 밝은 부분을 좀 강조해서 보겠다.
- 오른쪽 그래프의 경우, k부분에서 밝기가 이산적으로 바뀜.
- k 이하의 밝기는 전부 무시하겠다.
- r=k 지점을 임계점(Threshold)으로 볼 수 있음.
Image Negatives

s = T(r) = L - 1 - r- r은 [0, L - 1] 범위.
- T는 기울기가 -1인 직선 형태가 나옴.
- 밝은 애들은 어둡게, 어두운 애들은 밝게 나옴.
Log Transformation


s = T(r) = clog(1+r)- c는 L-1일 때 L-1이 나오도록 조정하기 위한 상수. (ex. 255 → 255)
- 약간 밝은(또는 어두운) 애들이 더 밝게 나옴.
- 원래 밝은 점들은 여전히 밝게 유지됨(좀 더 밝아지긴 함).
- 충분히 밝아지면 더 밝아져도 덜 밝아진걸로 인식된다.
Power-Law (Gamma) Transformations
Gamma Transformation
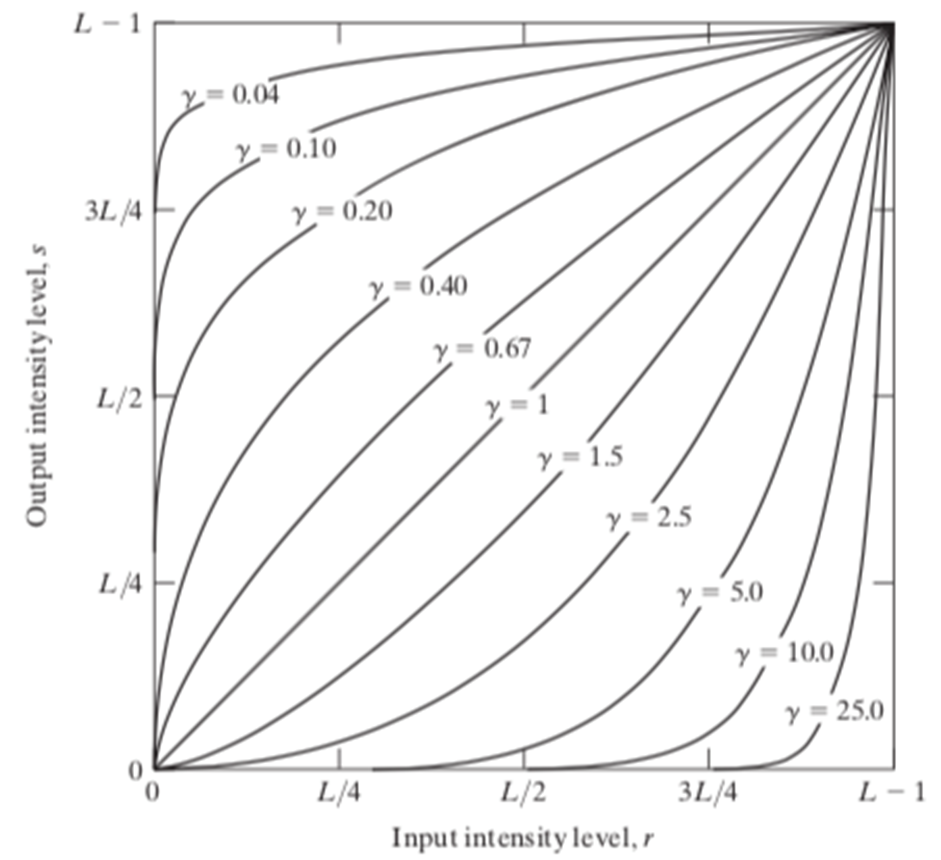
s = T(r) = c*(r^𝛾)𝛾 = 0.2. 정도면 아까 로그랑 얼추 비슷한 함수가 나옴.- 보통 𝛾을 [0, 1], c를 1로 둠.
- 목적은, 어두운 부분을 더 잘(더 밝게) 보고 싶으면 감마를 1보다 작게 두고,
- 밝은 부분을 선별하고 싶으면(어두운 부분을 덜 잘(덜 밝게) 보고 싶으면) 감마를 1보다 크게 두면 됨.
- 이러한 변환을 ‘감마 변환’이라 부름. 로그 변환보다 더 일반적인 버전.
Monitor response

- 우리 모니터에서, 만약 0.5라는 밝기가 주어지면, 몇 밝기를 출력하면 좋을까?
- 베버의 법칙에서, 자극의 크기가 조금 커진 걸 잘 느끼려면, 초기 밝기가 작아야 함.
- 베버의 법칙: 어두운 부분의 밝기 차이는 더 민감하게 인식하는 반면, 밝은 부분은 비슷한 변화에도 덜 민감하게 인식함.
- 즉, 밝은 곳에서 조금 더 밝아진 건 잘 인식을 못함.
- 따라서, 어두운 곳에선 조금만 밝아져도 사람은 차이를 크게 느낄 테니 그런 지점들을 잘 신경써야 함.
- 또한, 밝은 곳에선 좀 빠르게 확확 밝아져야 인식이 잘 됨.
- 즉, 감마가 1보다 큰 감마 변환을 먹여주면 좋을 것 같다!
- 따라서, 모니터에 출력될 땐 감마 변환을 먹여서 출력됨.
𝛾 = 2.2.- 어두운 부분은 더 어둡게 해주고, 밝은 부분은 빠르게 밝아지게 해둠.
- 해당 과정을 선형화(Linearization)이라고 함.
- 이미지 파일은 이와 반대로 역감마 변환을 먹여서 저장됨.
𝛾 = 1/2.2.- 이 보정이 수행되어 파일에 저장되는 이미지를 원본 이미지라고 보면 됨.
- 즉, 쉽게 말해, 원본 이미지 = 파일에 저장되는 이미지임. 근데 이 상태로는 사람이 볼 때 좀 불편하니까, 감마 변환을 먹여서 모니터에 출력하는 거임. 따라서 이걸 다시 파일로 저장할 땐, 역감마 변환을 먹인다 이 소리임.

- 위 사진에서 왼쪽 사진은
𝛾 = 1/2.2인 역감마 변환, 오른쪽 사진은𝛾 = 2.2인 감마 변환의 과정을 보여 줌.
Piecewise-Linear Transformation

- 저 (r1, s1), (r2, s2)등의 점들을 사용해 선분(line segment)들로 곡선 T를 정의하면 좀 더 성능이 좋을 수도 있음.
- 즉, 우리의 곡선 T를 단일한 연속적인 비선형 함수가 아니라, 여러 개의 직선 구간으로 나눠서 나타낼 수 있음.
- 단순한 선형 변환:
s = a*r + b- a는 대비(Contrast) 또는 gain이라 부름.
- → 어두운 곳과 밝은 곳의 차이를 얼마나 줄 거냐. 입력이 얼마나 과장되거나 축소되냐.
- 대비가 클수록 이미지에서 밝고 어두운 부분이 더 뚜렷하게 구분됨. 반대로 대비가 작을수록 이미지의 밝기 변화가 더 평평하게 보임.
a > 1: 입력값에 비해 더 빠르게 변화하는 응답을 의미함. 즉, 입력 값의 작은 변화가 출력에서 더 크게 확대되어 나타남. 이는 대비를 높이는 효과를 줌.- 예: 입력 값이 50에서 55로 변화하면, 출력 값은 더 큰 변화 (예: 100에서 110)로 확대됨.
a < 1: 입력값에 비해 응답이 더 느리게 변화하는 것을 의미함. 즉, 입력 값의 큰 변화가 출력에서 더 작은 변화로 나타남. 이는 대비를 낮추는 효과를 줌.- 예: 입력 값이 50에서 55로 변화해도, 출력 값은 그보다 적은 변화 (예: 100에서 102)로 나타남.
- b는 명도(Brightness) 또는 bias라 부름.
- → 전체적으로 더 밝게 해주거나 어둡게 해줌.
- 명도가 크면 이미지는 전체적으로 더 밝아지고, 명도가 작으면 이미지는 전체적으로 더 어두워짐.
- a는 대비(Contrast) 또는 gain이라 부름.


- 왼쪽 사진은 밝은 건 덜 밝고 어두운 건 덜 어두워서 이걸 보정해주고 싶음.
- → 중간 범위의 대비를 높이는 오른쪽의 선형 변환을 적용해 줘서 대비를 높여줌.


- 혈관 부분만 보고 싶은데 혈관이 일정 범위 이내의 밝기값을 가진단 걸 알고 있으면,
- → 오른쪽처럼 특정 밝기값을 가진 픽셀만 남기면 됨.
- 저걸 밝기 슬라이싱(Intensity slicing)이라고 부름.
- 어떤 T를 쓰냐에 따라 두 번째처럼 할 수도, 세 번째처럼 할 수도 있음.


- 비트 평면 슬라이싱
- 보통 8비트로 한 픽셀의 밝기를 표현하니,
- 각 픽셀 값이 1인 경우를 평면으로 표시해보자!!
- ex.
10000000, 01000000, 00100000, …, 00000001에 해당하는 평면들- 7비트(상위 비트) 평면 → 가장 중요한 구조를 나타냄 (전체적인 형태 유지)
- 0~2비트(하위 비트) 평면 → 노이즈나 작은 변화가 많음
- 사용 이유
- 이미지 압축
- 하위 비트는 삭제 가능
- 엣지 검출
- 상위 비트만 사용하면 강한 대비를 가진 엣지 강조 가능.
- 워터마크 삽입
- 하위 비트를 조작하여 워터마크 삽입 가능.
- 이미지 압축
Histogram Processing
Image Intensity Histogram

- 저 이미지는 굉장히 유명함. 레나라는 여성분 사진. 비젼 쪽에서 굉장히 많이 등장하는 사진.
- 이 사진은 밝기 히스토그램을 그려보면 얼추 일정함.

- 얘는 보면 밝기가 전반적으로 어두움. 즉, 어두운 이미지임.

- 얘는 보면 밝기가 전반적으로 밝음. 즉, 밝은 이미지임.
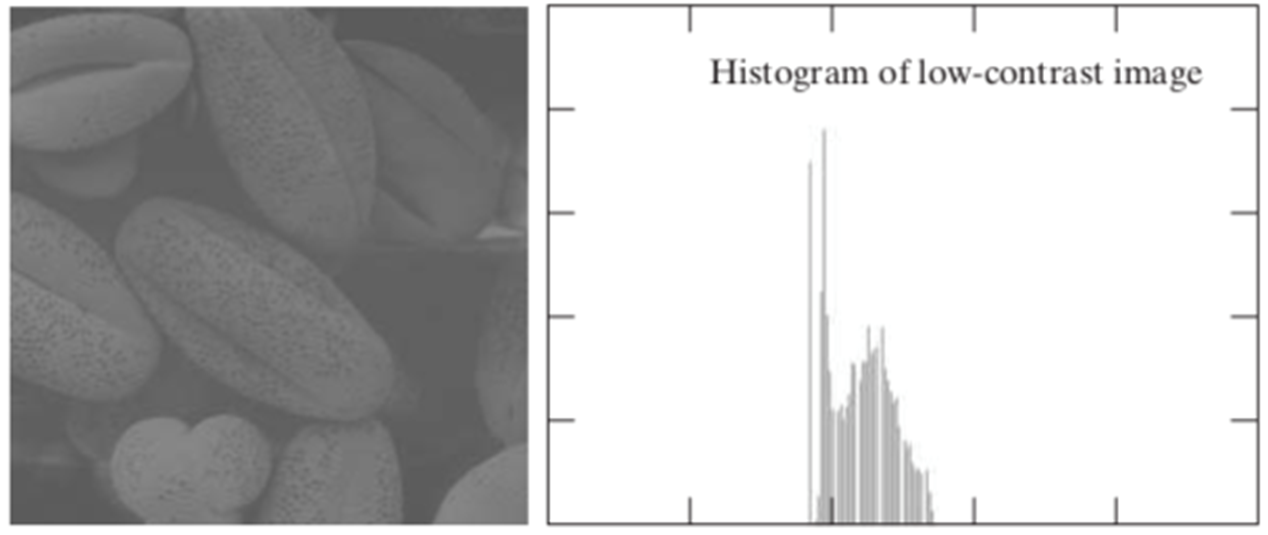
- 얘는 너무 밝기가 중간에 몰려 있음. 즉, 대비가 낮은 이미지임.
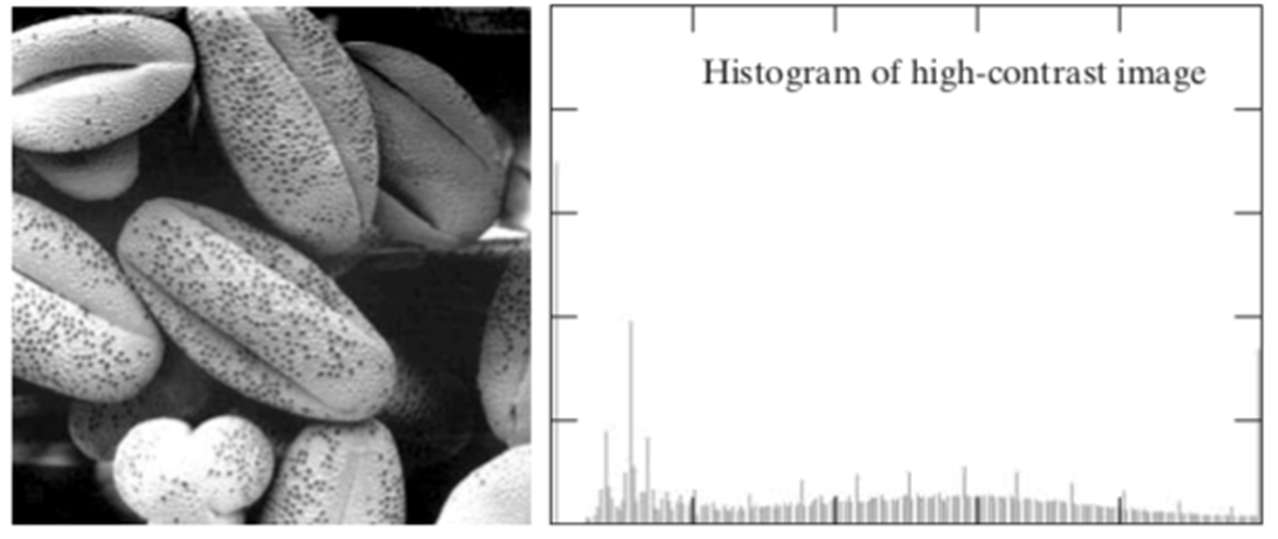
- 얘는 밝기가 적절히 퍼져있음. 즉, 대비가 높은 이미지임.
- 저런 식으로 밝기가 균등하여 대비가 높은 이미지를
좋은 이미지또는대비가 좋은 이미지또는히스토그램이 균등한 이미지라고 ****부를 거임.
참고) U자형 히스토그램??
- 대비는 어두운 영역과 밝은 영역 간의 차이가 얼마나 뚜렷하게 드러나는지를 의미함.
- U자형 히스토그램: 극단적인 어둡고 밝은 영역이 많아 매우 대비가 강해지나, 중간톤 정보가 부족할 수 있고 디테일이 손상됨.
- 균등한 히스토그램: 전체 밝기 범위를 고르게 사용하여, 세부 디테일과 자연스러운 대비를 유지함.
- 따라서, U자형 히스토그램이 더 대비가 좋다고 할 순 있으나, 좋은 이미지라고 부르기는 어려움.
- 따라서 우리는 균등한 히스토그램을 가진 이미지를 좋은 이미지 또는 대비가 좋은 이미지라고 부를 것임.
Histogram Equalization
- 우리는 저런 좋은 이미지를 만드는 T를 구하고 싶다.
- 복습)
s=T(r): 0≤ r ≤L-1 
- 가정:
- T는 강한 단조 증가 함수.
- 즉, 위 두 그래프 중 오른쪽과 같은 형태만 인정하겠다는 거임.
- 즉, 우리는 일대일 대응 함수 T만을 인정할 거임.
- 결과 범위는 [0, L-1] 사이.(
0≤ T(r) ≤L-1)
- T는 강한 단조 증가 함수.
Histogram as PDF
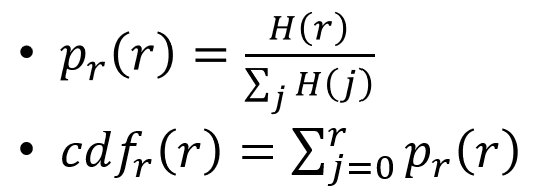

- 각각 pdf, cdf(확통에서 배운 거!)
p_r(r):- 전체 이미지에서 밝기가 r인 픽셀이 차지하는 비율을 의미함.
- 여기선 확률의 정의에 부합하므로 확률로도 볼 수 있고, 따라서 p_r(r)을 r의 pdf라고 할 수 있음.
cdf_r(r):- 전체 이미지에서 밝기가 r 이하인 픽셀들이 차지하는 누적 비율을 의미함.
- 따라서, cdf를 보면 자기보다 어두운 놈들 비율을 볼 수 있음.
Better contrasted image

- pdf가 상수함수에 가까운, even한 형태가 나와야 대비가 좋은 이미지가 됨(아까 대비가 좋은 이미지의 히스토그램 참고)
- 그렇게 even하게 상수값 1/L-1을 가지면, cdf는 그걸 계수로 하는 직선이 됨.
- 반대로 cdf가 증가하는 직선 형태가 나오면, pdf는 상수함수 형태가 나올 것이다.
Implementation

- 나보다 어두운 놈들의 개수를 다 세서, 그거에 따라 자기 밝기를 결정하겠다!
- 즉, 특정 점의 밝기를, ‘자신보다 어두운 놈들의 비율’로 정하겠다.
- 그걸 구현한 함수가 T.
- H는 히스토그램.
- 전체 이미지 크기(픽셀 개수)인 NM이 분모로 들어감.
- 즉, 밝기가 r인 픽셀들을 함수 T에 넣어서, 밝기를 s로 재조정해주는 거임.
- 이 때 T가 r→s 매핑하는 데 쓰는 게 r의 cdf임. 즉, cdf_r(r)에다가 r을 넣고, 거기에 L - 1을 곱해준 값으로 s를 정하겠다!
- 이렇게 하는 이유는, cdf가 s / (L - 1)꼴이 나오기를 내가 원하고 있기 때문임. 그래야 히스토그램 즉 pdf가 균등해질 거니까.
- 이 때 T가 r→s 매핑하는 데 쓰는 게 r의 cdf임. 즉, cdf_r(r)에다가 r을 넣고, 거기에 L - 1을 곱해준 값으로 s를 정하겠다!
- 이렇게 히스토그램을 균등하게 만들어서 대비를 높이는 기법을 히스토그램 이퀄리제이션(Histogram Equalization)이라고 부름.
- 위 변환을 통해, 밝기가 r인 픽셀들의 밝기가 일괄적으로 s로 바뀜.
Histogram Equalization Results
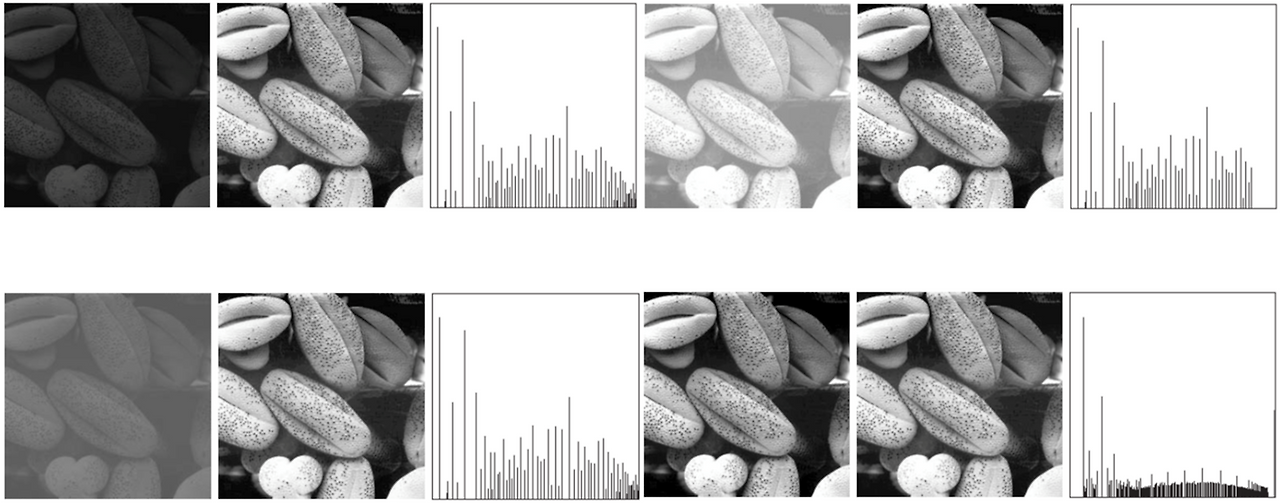
- 그러면 위처럼, 아까는 너무 어둡거나 너무 밝거나 대비가 작거나 했던 이미지들도 비교적 대비가 좋게, 균등한 히스토그램이 나옴.
- 대비가 컸던, 이미 균등했던 히스토그램도 여전히 균등.
Other Histogram Transformation
- 히스토그램 매칭(Histogram matching)
- 주어진 이미지의 프로필(profile)을 참고해서 히스토그램을 만드는 기법.
- 즉, 이미 주어진 어떤 히스토그램과 비슷하게 히스토그램을 만들고자 하는 거임.
- 예를 들어, 특정 조명 조건에서 촬영된 이미지의 히스토그램을, 다른 조명 조건에서 촬영된 이미지와 비슷하게 만드는 데 사용할 수 있음.
- 주어진 이미지의 프로필(profile)을 참고해서 히스토그램을 만드는 기법.
- 지역 히스토그램 균등화(Local (Adaptive) Histogram Equalization ,AHE)

- 기존에 수행한 Global Histogram Equalization(전역 히스토그램 평활화)은 이미지 전체의 히스토그램을 균등화하여 전체적인 대비를 좋게 만들지만, 지역적 대비를 개선하는(높이는) 데는 한계가 있음. 그래서 나온 방식.
- 전체적으로는 밝은 색 어두운 색이 균등히 포함되어 있어서 대비가 좋은데, 부분적으로는 특정 색(밝기)들이 몰려 있어 대비가 안좋을 수 있음.
- 작동 방식:
- 이미지를 작은 window (예: 8x8 픽셀, 16x16 픽셀 등)으로 나누고, 각 window에 대해 독립적으로 히스토그램 균등화를 적용함.
- 그럼 부분적으로 균등화가 일어나기 때문에, 아까와 같은 부분적으로 대비가 안좋을 가능성이 줄어듦.
- 그 후, overlapping되는 각 window들의 결과들을 결합하여 이미지 전체에 적용함.
- → 겹치는 영역에서 값이 부드럽게 이어지도록 하는 거임.
- 이미지를 작은 window (예: 8x8 픽셀, 16x16 픽셀 등)으로 나누고, 각 window에 대해 독립적으로 히스토그램 균등화를 적용함.
- 기존에 수행한 Global Histogram Equalization(전역 히스토그램 평활화)은 이미지 전체의 히스토그램을 균등화하여 전체적인 대비를 좋게 만들지만, 지역적 대비를 개선하는(높이는) 데는 한계가 있음. 그래서 나온 방식.
'AI & Data > 컴퓨터 비전(CV)' 카테고리의 다른 글
| [영상처리] Ch3.2. Spatial Filtering (0) | 2025.04.07 |
|---|---|
| [영상처리] Ch2. Human Vision (0) | 2025.03.24 |
| [영상처리] Ch1. Introduction. (0) | 2025.03.10 |


