Digital Image Processing, 4Th Edition: Rafael C. Gonzalez, Richard E. Woods
본 글은 위 교재를 주교재로 한 학교 '영상처리(Image Processing)' 수업을 들으며 공부한 내용을 정리한 글입니다.
해당 글은 개인 공부 및 교육 목적으로 작성하였으며, 일부 교재에 첨부된 사진(또는 교재에서 강의노트로 첨부된 사진)들을 포함하고 있습니다.
교재 출처 사진을 최소화하고자 블로그에는 핵심 사진을 제외하곤 옮기지 않은 사진들도 있습니다. 따라서 고의로 누락한 사진들이 존재하며, 해당 사진들을 언급하는 내용이 있을 수 있습니다. 누락한 사진들은 직접 교재를 참고해 주세요.
혹시 문제가 있다면, 댓글 남겨주시면 빠른 시일 내에 확인 후 적절한 조치를 취하겠습니다.
Contents
- Spatial Filtering Fundamentals
- Smoothing Spatial Filters
- Sharpening Spatial Filters
- Combining Spatial Enhancement
Spatial Filtering Fundamentals
Spatial Filtering

- 우리가 지금까지 밝기 변환에선, 아웃풋 픽셀 밝기를 위해 인풋 픽셀 밝기를 하나만 사용했잖음. 이젠 그 주변의 픽셀들(이웃들)의 밝기도 보자.

- 이를 위해 위와 같은 합성곱 연산을 수행.
- w(s, t)는 (s, t) 위치의 필터(커널) 값.
- 필터는 a x b 크기
- 인풋 픽셀은 (x, y) 픽셀
- 아웃풋 픽셀 밝기는 g(x, y)
Similar Concepts
- 이런 공간 필터링은
- 상관관계(Correlation)과도 비슷해 보이고,
- 합성곱(Convolution)과도 비슷해 보임.

- 위가 일반적인 연속공간 위에서의 합성곱 공식.
- 우리의 공간 필터링 함수식 또한 이산공간 위에서의 합성곱 공식 정도로 일반화해도 크게 상관없을 듯함.
Padding
- 근데, 저 경계의 픽셀을 가지고 아웃풋 픽셀 밝기를 만들려는데, 주변 픽셀들(이웃들)이 부족하잖음!!
- 6x6 이미지에 3x3 필터로 필터링을 돌리면, 결과 이미지는 4x4 크기가 돼버림…
- 우리는 원본 이미지의 크기를 유지하고 싶음 ㅠㅠㅠㅠ
- → padding을 추가하자.
- 마치 경계 바깥에 이미지가 추가로 있다는 가정.
- 가상의 픽셀들(virtual pixels)을 원본 이미지의 네 엣지들에 추가하는 거임.
- 패딩은 여러 방법이 있음.
- Constant Padding
- 그냥 고정된 상수로 채우는 거
- e.g. 제로 패딩
- Replicate Padding
- 그 엣지에 있는 픽셀값들 그대로 복사하는 거
- Mirror(Reflection) Padding
- 경계 선을 기준으로 거울처럼 픽셀값을 반사시켜 복사하는 거임.
- Constant Padding
Smoothing Spatial Filters
Smoothing(스무딩)
- 목적:
- 이미지를 좀 더 부드럽게 만들고,
- 노이즈를 억제하고,
- 너무 많이 등장하는 놈을 제거하자
Averaging Filter(평균 필터)

- 스무딩을 하려면 주변값을 써서 뭉개야 하는데,
- 그 중 제일 쉬운 게 이웃들 평균내서 결과내는 거임.
- 이러한 규칙으로 필터링을 수행하는 필터를 평균 필터(Averaging Filter)라 부름.
- 평규 필터는 박스 필터(box filter)라고도 불림.

- 저기에 1/9를 Operation 또는 Filter value 정도로 부름.
Box Filter


- 보면, 그냥 뭉개지기만 한 게 아니라, 이미지의 경계 부근에 진한 선같은게 생김.
- 이거 왜 생겼는진 좀 나중에 말한다고함.
- 아마 zero padding을 주다 보니까 경계 픽셀들의 평균이 낮아져 어두운 테두리가 생기는 거일듯.
- 근데 이렇게 평균으로 뭉개버리니까 아직 좀 어색한 것 같음. 개선할 수 없을까?
- → 그냥 무작정 평균내지 말고,
- 아래처럼 인풋 픽셀과의 위치 관계에 따라 가중치(weight)를 다르게 주자!
Weighted Averaging Filter
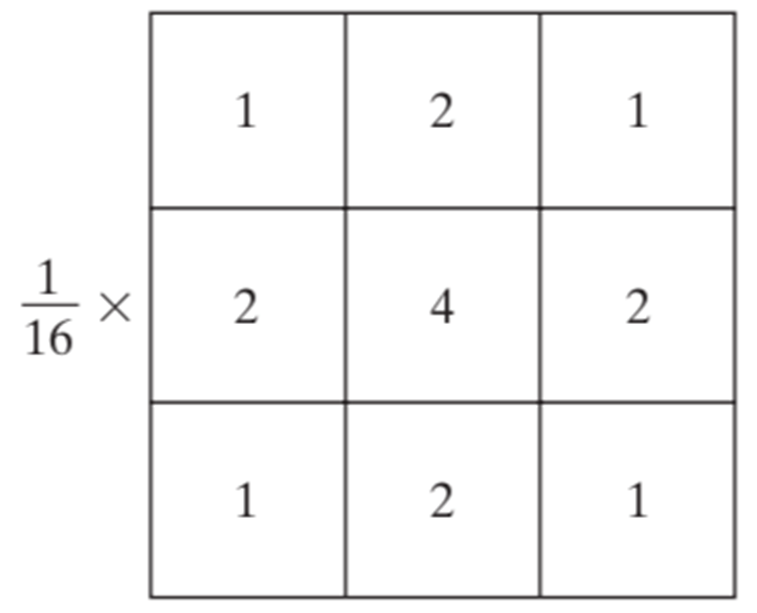
- 인풋 픽셀과의 위치 관계에 따라 가중치(weight)를 다르게 줌.
- 그런 필터를 가중치 평균 필터(Weighted Averaging Filter)라고 함.
가우시안 필터(Gaussian Filter)

- s: s축으로의 이동
- t: t축으로의 이동
- 따라서, 분자는 저건 유클리디안 거리의 제곱임.
- 그리고 저 분산으로 나눠줌.
- 교수님 왈) 저 식 외우지 마라.
- 대충, 정규분포처럼 생겨먹은 가중치 평균 필터를 가우시안 필터라고 하고, 그걸 써보겠다!!

- 왼쪽 사진은 원본 사진에다가 노이지를 고의로 집어넣은 사진임.
- 저 PSNR은 노이즈를 측정하는 측도임. 단위는 dB. 작을수록 사진에 노이즈가 많음.
- 왼쪽 사진은 노이지 측도가 39.1dB정도 되어 노이즈가 껴있는 상태임.
- 근데, 그 노이즈 낀 이미지에 가우시안 필터를 먹이니까, 노이즈 측도가 67.9dB로 노이즈가 줄어들고 이미지가 좋아졌단 거임.
- 우리가 보기엔 저게 좋아진 건진 모르겠지만, 노이즈의 관점에서 보면 노이즈가 줄어들었으니 사진이 좋아진 거.'
GPT) 박스 필터 사용 단점 정리
2초 동안 이성 처리 완료
박스 필터는 간단하고 연산 비용이 낮다는 장점이 있지만, 이미지 처리에서 사용 시 여러 가지 단점이 있습니다. 여기서는 박스 필터의 주요 단점을 정리해 보겠습니다.
1. 균일한 가중치로 인한 부자연스러운 블러
- 동일한 가중치:
- 박스 필터는 커널 내부의 모든 픽셀에 동일한 가중치(예: 1N\frac{1}{N}N1)를 부여하기 때문에, 중심과 주변을 구분하지 않습니다.
- 결과:
- 이로 인해 이미지의 모든 영역이 고르게 혼합되어, 경계나 세부 구조가 부드럽게 보존되지 않고 뭉개지는 효과가 나타납니다.
2. 경계 보존력 부족
- 에지 보존 미흡:
- 경계(엣지) 부분에서도 동일한 가중치가 적용되므로, 선명한 경계가 흐려지고 모서리가 둔탁해집니다.
- 결과:
- 중요한 디테일이나 객체 경계가 희미해져서 후속 처리(예, 객체 검출, 경계 추출 등)에서 부정적인 영향을 줄 수 있습니다.
3. 인공적인 효과 및 아티팩트
- 모서리 효과:
- 균일하게 평균 내는 방식은 주변 픽셀들의 갑작스런 변화에 대해 비자연적인 효과(예, “블록” 형태의 아티팩트)를 발생시킬 수 있습니다.
- 주파수 도메인 영향:
- 박스 필터는 주파수 스펙트럼에서 고주파 성분을 충분히 억제하지 못하여 링잉(ringing) 효과나 불필요한 노이즈가 생길 가능성이 있습니다.
4. 낮은 시각적 품질
- 부드러움 부족:
- 가우시안 필터 등 다른 블러 필터에 비해, 박스 필터는 시각적으로 부드럽고 자연스러운 효과를 내기 어렵습니다.
- 비선형 특성 미반영:
- 인간의 시각 시스템은 밝기 변화에 대해 비선형적 반응을 보이는데, 박스 필터는 이러한 특성을 고려하지 않아 결과가 부자연스러울 수 있습니다.
5. 잡음 및 텍스처 왜곡
- 잡음 제거 한계:
- 박스 필터는 단순 평균 값을 계산하므로, 원치 않는 잡음이나 미세한 텍스처가 제거되는 대신, 일부가 그대로 남거나 비정상적인 블러 효과가 나타날 수 있습니다.
- 텍스처의 세부 정보 손실:
- 텍스처나 세밀한 디테일이 있는 영역에서는 경계가 불분명해져 중요한 정보가 소실될 수 있습니다.
요약
박스 필터는 계산이 간단하고 빠르지만, 균일한 가중치로 인해 다음과 같은 문제들이 발생합니다:
- 경계 및 세부 구조의 모호화:
- 모든 영역에 동일 가중치 적용 → 경계가 흐려짐
- 인공적 아티팩트 발생:
- 주변 픽셀 변화 무시 → 비자연적인 효과 및 링잉
- 시각적 품질 저하:
- 자연스러운 블러 효과 부족, 잡음 및 텍스처 왜곡
이러한 단점 때문에 고품질의 블러 효과나 디테일 보존이 필요한 응용에서는 가우시안 블러 같은 다른 필터가 선호됩니다.
필요하시면 각 항목에 대해 더 자세한 이론이나 예시, 이미지 비교 등도 추가로 설명드릴 수 있습니다. 더 궁금한 점 있으신가요?
o3-mini
나의 말:
박스 필터의 ghost line 현상
ChatGPT의 말:
10초 동안 이성 처리 완료
박스 필터를 사용할 때 나타나는 ghost line 현상은 주로 다음과 같은 이유로 발생합니다:
- 균일 가중치와 갑작스러운 경계 처리
- 박스 필터는 모든 픽셀에 동일한 가중치(평균)를 적용합니다.
- 이로 인해 이미지의 강한 경계(에지) 부근에서도 주변 값들을 동일하게 평균 내어, 실제 경계와 약간 어긋난 영역에서도 경계선 모양의 잔상(ghost line)이 생길 수 있습니다.
- 필터의 "직사각형" 형태와 주파수 응답
- 박스 필터의 커널은 직사각형 형태이며, 주파수 영역에서는 sinc 함수(sin(x)/x)와 유사한 응답을 가지게 됩니다.
- sinc 함수는 주된 봉우리(main lobe) 외에도 여러 개의 측면 봉우리(side lobes)를 갖는데, 이 측면 봉우리가 필터링 후 이미지에 잔류 효과로 나타나 ghost line 현상을 유발할 수 있습니다.
- 패딩 방식의 영향
- 경계 부분에서 박스 필터를 적용할 때, 단순 복제(replicate)나 반사(reflect) 방식으로 패딩하면 인위적인 경계 효과가 더 두드러질 수 있습니다.
- 이로 인해 경계 부근에서 ghost line과 같이 본래의 경계 외에 추가적인 선이 나타나는 결과가 생길 수 있습니다.
- 낮은 공간 해상도 및 aliasing
- 박스 필터는 공간에서 픽셀값들을 단순 평균하여 처리하기 때문에, 미세한 변화나 aliasing 현상을 완화하는 데 한계가 있습니다.
- 특히 고주파 성분이 많은 이미지에서 이러한 문제로 인해 ghost line과 같은 아티팩트가 발생할 가능성이 높아집니다.
요약
- 박스 필터는 모든 픽셀에 동일한 가중치를 주어 경계 부근의 변화에 민감하지 않으며,
- 직사각형 커널의 sinc 형태 주파수 응답 때문에 측면 봉우리가 생겨
- 경계 주변에 ghost line 현상이 나타날 수 있습니다.
이러한 이유로, 더 자연스럽고 부드러운 블러 효과를 위해서는 가우시안 필터와 같은 가중치가 중심에서 점차 감소하는 필터가 주로 사용됩니다.
필요하면 ghost line 현상이 실제 이미지에서 어떻게 나타나는지, 실험 예제나 시각적 비교 자료도 추가로 설명해드릴 수 있습니다. 추가 문의 있으시면 말씀해주세요!
GPT) 박스 필터 vs 가우시안 필터 비교
- 가우시안 필터 vs 박스 필터 비교를 깔끔하게 정리해 드릴게요.
🎯 가우시안 필터 vs 박스 필터구분가우시안 필터박스 필터 (평균 필터)원리 픽셀 간 거리 기반 가중합 (멀수록 가중치 낮음) 모든 픽셀을 동일 가중치로 평균 블러 품질 자연스럽고 부드러움, 가장자리 덜 뭉개짐 비교적 인위적인 블러, 경계 부분 흐림 큼 엣지 보존 상대적으로 엣지 잘 보존 (선형적으로 감소) 엣지 흐림 심함 (모든 픽셀 평균이므로) 계산 비용 더 복잡 (가중치 계산) 간단하고 빠름 (그냥 평균) 노이즈 제거 랜덤 노이즈 제거 효과가 좋음 노이즈 제거는 되지만 약간 덜 효과적 필터링 효과 제어 시그마 값으로 블러 강도 세밀하게 조절 가능 필터 크기로만 제어 (조절 한계) 사용 용도 이미지 블러, 엣지 전처리, 노이즈 감소 간단한 블러, 연산량 줄일 때 빠르게 사용
🧩 요약- 품질: 가우시안 필터가 더 자연스럽고 품질 좋음.
- 속도: 박스 필터가 빠름.
- 엣지 보존: 가우시안 필터 우위.
- 조절성: 가우시안은 시그마로 세밀하게, 박스 필터는 크기로만.
- 노이즈 제거: 가우시안이 더 효과적.
🎨 비유- 가우시안 필터: 미술 시간에 부드럽게 스머징 하는 느낌.
- 박스 필터: 스폰지로 쓱 문지르는 느낌.
그래서,- 빠른 처리 + 간단한 흐림이면 박스 필터
- 품질 + 자연스러운 흐림, 노이즈 감소까지 원하면 가우시안 필터
- 입니다!
---
원하시면 실제로 이미지 두 개 비교하는 시각적 예제도 드릴 수 있어요 🔍
(가우시안 vs 박스 필터, 같은 크기로 적용하면 결과가 꽤 다릅니다!)GPT) 가우시안 필터가 노이즈를 박스 필터보다 더 잘 제거하는 이유
- salt-and-pepper noise (검은 점, 흰 점)
- Gaussian noise (정규분포형 노이즈)
- 이런 노이즈는 픽셀 하나 또는 근처 픽셀들 값이 갑자기 튀는 현상인데요.
박스 필터는?→ 그래서 엣지나 노이즈 구분 없이 무조건 평균.
- 노이즈는 주변 값들과 많이 다를 수 있는데,
- 박스 필터는 노이즈 하나가 전체 평균에 과하게 영향을 줍니다.
- 결과:*
- 노이즈는 조금 줄지만, 엣지랑 디테일도 같이 흐려짐.
가우시안 필터는?
- 노이즈는 대부분 랜덤하고 국소적인 튐이기 때문에,
- 중심값이 노이즈가 아닐 경우, 주변 노이즈 픽셀들의 영향이 줄어듭니다.
- 설령 중심이 노이즈더라도 주변 정상 픽셀들이 더 큰 영향을 미쳐 평균이 잘 잡힙니다.
- 결과:*
- 노이즈는 줄이고, 엣지는 상대적으로 보존할 수 있게 됨.
- 노이즈는 국지적이지만, 엣지는 더 넓게 분포하므로 가우시안이 더 유리!
요약!
필터노이즈 제거 능력이유| 박스 필터 | 보통 | 노이즈랑 엣지를 구분 못 하고 다 같이 평균 |
| 가우시안 필터 | 더 좋음 ✅ | 중심부 위주로 가중합 → 노이즈 영향을 줄이고 자연스럽게 평균화 |
비유 🎨
- 박스 필터: 내 주위 사람이 시끄럽든 조용하든 모두 똑같이 신경 씀.
- 가우시안 필터: 가까운 사람 말은 신경 많이 쓰고, 멀리 있는 사람 말은 별로 신경 안 씀.
- → 시끄러운 노이즈가 멀리 있으면 영향이 작음!
- 가우시안 필터는 중심부 픽셀에 가중치를 더 많이 주고, 멀어질수록 가중치를 줄여요.
- 박스 필터는 주변 픽셀을 무조건 똑같이 평균내버려요.
- 이미지의 노이즈는 주로 랜덤하게 튀는 밝기 값이죠.
- 좋은 질문이에요. 👍 아주 본질적인 부분을 짚으셨어요!
정리)가우시안 필터에서 시그마가 크고 작은 것의 의미.
시그마는 분포의 '퍼짐 정도'를 결정하는 값으로,
시그마가 작으면: 중심 픽셀에 매우 큰 가중치를 주고 주변 픽셀은 거의 무시되어, 블러 정도가 약해짐. 엣지 디테일이 잘 보존됨.
시그마가 크면: 중신 픽셀뿐 아니라 주변도 꽤 큰 가중치를 주어, 블러 정도가 강해짐. 이미지 전체가 부드럽게 퍼지고, 엣지 디테일이 많이 사라짐. 점점 박스 필터에 가까워짐.
GPT)필터의 크기가 크고 작은 것의 의미.
- 필터 크기 = "영향을 주는 범위"
- 필터 크기가 크다→ 더 많이 퍼진 블러링 / 더 강한 노이즈 제거 / 그러나 엣지도 많이 뭉개짐 / 점점 박스 필터에 가까워짐
- → 더 넓은 영역의 픽셀들을 평균하거나 가중합해서 사용
- 필터 크기가 작다→ 가벼운 블러링 / 원본 유지에 가까움 / 그러나 엣지는 많이 보존됨
- → 주변 몇 픽셀만 사용
- 📏 필터 크기가 크고 작은 것의 의미
--- ## 🎯 **조금 더 기술적으로** | 필터 크기 작음 | 필터 크기 큼 | | --- | --- | | 영향 범위 작음 (local) | 영향 범위 큼 (global 에 가까움) | | 흐림 정도 약함 | 흐림 정도 강함 | | 노이즈 제거 약함 | 노이즈 제거 강함 | | 디테일 유지 | 디테일 손실 가능성 | | 에지 보존 상대적으로 잘 됨 | 에지도 많이 흐려짐 | | 속도 빠름 (계산량 적음) | 속도 느림 (계산량 많음) | --- ## 🎨 비유 - **작은 필터**: 확대경으로 작은 부분만 다듬는 것 - **큰 필터**: 넓은 붓으로 대충 훑는 것 (디테일이 사라짐) --- ## 📸 실제 이미지 효과 | 크기 | 박스 필터 | 가우시안 필터 | | --- | --- | --- | | 작음 (3x3) | 약한 흐림 | 약한 흐림 | | 큼 (15x15 이상) | 강한 흐림, 기계적 느낌 | 자연스럽고 부드러운 흐림 | --- ## 🧩 박스 vs 가우시안 관점에서도 - 박스 필터는 크기를 키울수록 뭉개짐이 아주 뚜렷함 (거친 느낌) - 가우시안 필터는 크기를 키우면 더 부드럽고 자연스럽게 블러링 → 하지만 둘 다 크기가 커지면 결국 **디테일 손실** 은 피할 수 없습니다. --- ## ⏱️ 참고: 필터 크기 vs 시그마 특히 가우시안 필터는 필터 크기뿐 아니라 **σ (시그마)** 값도 영향! - σ 크면 → 넓게 퍼짐 (크게 흐림) - σ 작으면 → 촘촘히 집중 (적게 흐림) 보통은 **필터 크기 ≈ 6 × σ** 정도로 맞추면 자연스럽습니다. (이건 실무 팁이에요 🔥) --- 정리하면! > 필터 크기가 크다 = 더 넓은 영역을 고려해서 더 많이 흐리고, 노이즈 제거 효과는 크지만, 디테일은 더 많이 잃는다. > ---
시그마 값, 필터 크기, 박스 필터 vs 가우시안 필터 막간 정리
→ 대략적으로, 가우시안 크기에서 시그마의 크기가 커지는 것과 필터의 크기가 커지는 게 비슷한 효과를 가진다고 보면 될듯.
→ 또한, 특히, 가우시안 필터의 시그마를 아주 크게 주면 "거의 박스 필터 비슷"해 보이는 느낌이 남. 즉, 비슷한 효과이긴 하나, 박스는 극단적으로 더 단순화된 케이스라고 볼 수 있음. 그러나 시그마를 키우면 가우시안의 종이 퍼지면서 점점 박스 필터 느낌이 나긴 하지만 완전히 같아지진 않음. 박스는 여전히 뚝 끊기는 형태.
→ 핵심은, 시그마 크기가 커지고 필터 크기가 커질 수록, 노이즈는 더 잘 제거되나 엣지 또한 더 잘 뭉개짐.
Separable Filter
- 특정 조건을 만족하는 필터를 가지고, ‘이 필터는 세퍼러블하다’ 라는 표현을 씀.
- 그니까, 2차원 필터가 주어지는데,
- 이 필터가 1차원으로 x방향 y방향 순서대로 필터링한 것과
- 그냥 원래대로 2차원 필터링한 것이
- 결과가 똑같다??
- → 그러면 이 필터는 세퍼러블(Seperable)하다고 부름.

- 위와 같은 예시가 있을 수 있음
- 오른쪽에 저게 원본 2차원 필터, 왼쪽은 그걸 x방향 y방향 필터로 뜯은 것
- 세퍼러블한 필터는, 필터의 디멘션 합을 m x n에서 m + n으로 뜯어 분해할 수 있어서,
- 당연히 세퍼러블한 필터가 더 좋음!!
- 단위연산이 덜 수행되니까 당연히 좋지!
- 우리가 배운 박스 필터, 가우시안 필터 등이 다 세퍼러블한 필터들임.
Order-Statistic (Non-linear) Filters

- 저렇게 무작위로 검정색, 하얀색 노이즈들이 껴있는 걸 salt and pepper noise라고 부름.
- 주변이랑 좀 그나마 비슷한 값을 가지는 노이즈가 아닌, 좀 극단적인 값을 가지는 노이즈들.
- 여기에 가우시안 필터링 등 해도 노이즈를 무시하기가 어려움. 오히려 주변 픽셀에 악영향만 끼침.
- 근데, 이거 픽셀의 대표값 뽑는 방식이, 지금처럼 (가중치 주든 말든) 평균도 있지만,
- ‘중앙값’은 어떨까?
- 중앙값 필터(Median Filter) 등장
- non-linear한 ordr-statistic 필터임.
- 만드는 과정에 곱하거나 더하는 linear한 연산이 포함되지 않음.
- 각 픽셀과 그 이웃 중에서 중앙값을 뽑음.
- 좀 극단적인 값들(outlier) 무시가 가능함.
- non-linear한 ordr-statistic 필터임.
- 이거 쓰면 zero padding시 외곽에 검정 선 생기는 것도 그 0 값이 선택되지 않는 경우가 많아질 것이므로 어느정도 완화가 될 것이나,
- 0이 추가되는 것 만으로도 중앙값 선택에 영향을 미치므로 실제 이미지보다 더 어두운 픽셀이 중앙값으로 선택될 가능성이 높아져 어두워지는게 완전 해결되진 않음.
- 그러나, 잘못 적용하면 사진이 떡질 수 있음(과장돼서 밋밋하게 나올 수 있음).
Sharpening Spatial Filters(엣지 검출 할 거임)
Derivatives(변화율)
- blur을 하면, 특히 엣지가 뭉개짐.
- 엣지의 정의는 나중에 다시 배우는데, 색깔이 일정하다가 갑자기 바뀌는 지점임.
- 즉, 색이 엣지에서 확 바뀌어야 하는데, 그렇지 못하고 변화가 점진적으로 나타남. 천천히 바뀐다. 즉, gradient가 완만해진다 또는 gradation이 생긴다.
- 따라서, 우리는 엣지의 색 변화를 더 많이 바뀌도록 해주면 더 선명하게 보이지 않을까?
- 즉, 우리는 엣지를 강조해주고 싶음. 다시 말해, 색 변화를 더 극적으로 만들어주고 싶음.
- 그러기 위해선 엣지의 위치를 찾아야 하고,
- 엣지의 위치를 찾으려면 gradient가 확 변하는 순간을 계산해야함. 즉 변화율을 계산해야함. 색이 많이 바뀌는 부분을 찾아내야함.

- 원래 continuous domain 상에서의 도함수(변화율)의 정의는 위와 같음.

- 그러나, 우리는 discrete domain 상에서 도함수를 정의해야함. 픽셀 좌표에 연속인 게 어딨어.

- 저렇게 이계도함수(변화율의 변화율)를 구해볼 수도 있음.
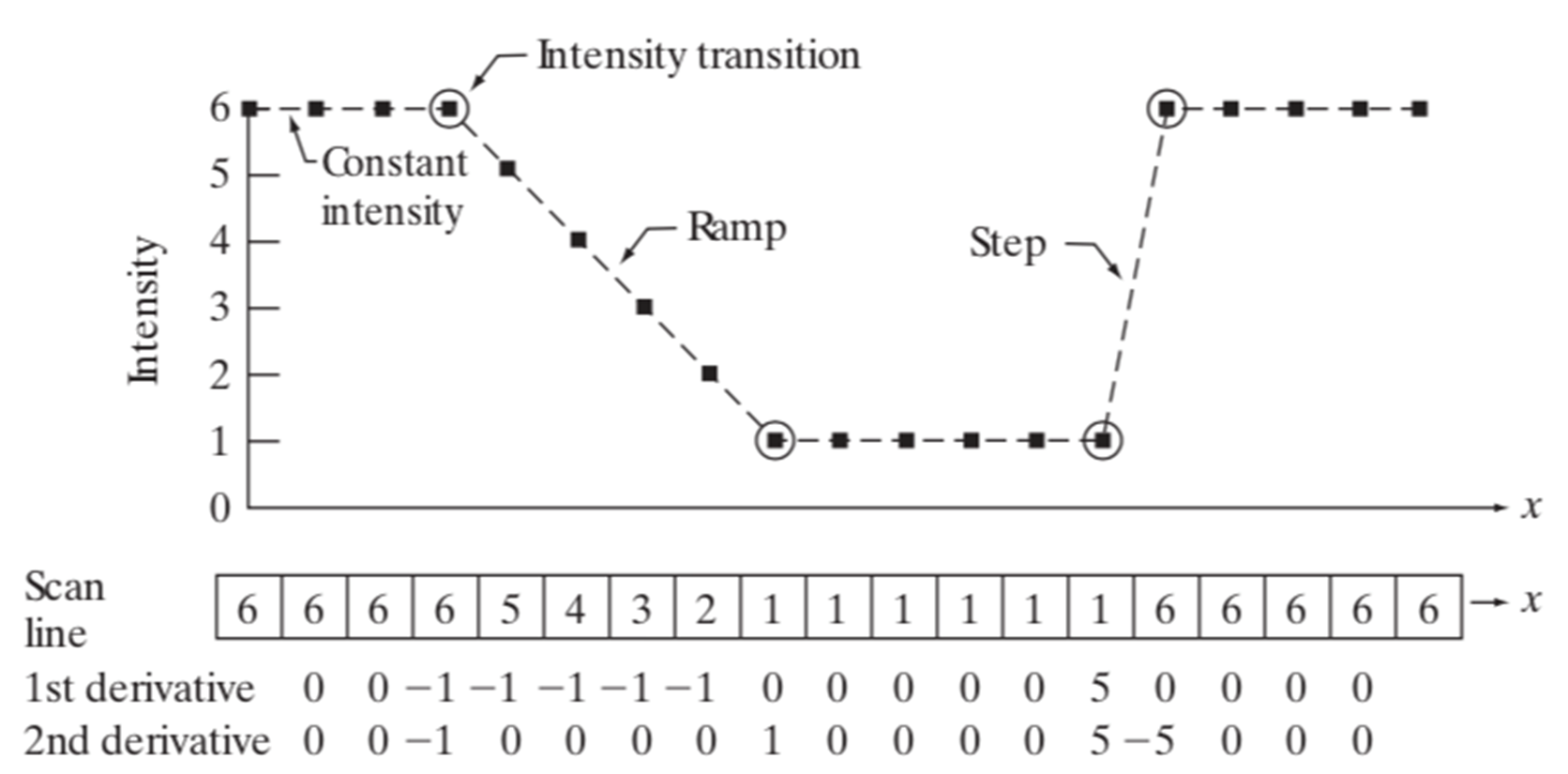
- scan line의 픽셀 좌표 x에 따라 밝기(intensity)의 변화를 표현한 그래프.
- 저 앞쪽에선 미분계수(미분값)가 0 나오다가, 내려가기 시작하면 -1 나오고,
- 다시 0 나오고, 그 다음에 양수 나오고 다시 0 나오겠지.
- 용어)
- Ramp: 밝기가 서서히 변하는 엣지. 또는 완만한 밝기 변화.
- Step: 밝기가 계단처럼 급격히 변하는 엣지. 또는 급격한 밝기 변화.

- 위는 도함수와 이계도함수의 값을 나타낸 것임.
- 보면, 이계도함수의 그래프가 0을 지나는 순간이 나타난단 거임.
- 저 순간을 zero-crossing하는 순간이라고 얘기하고,
- 이 때 밝기가 급격하게 변할 것이라고 예상 가능.
- 참고) 저거 계산할 때,
값(x) - 값(x - 1)로 계산한 거임. 도함수랑 이계도함수 둘 다.
도함수의 특징
- 일정한 밝기를 가진 영역에서는 0임.
- 즉, 같은 색이 계속되는 부분(ex. 단색 배경)에서는 변화가 없으니까 당연히 미분값이 0.
- step가 시작되는 지점(onset)에서는 0이 아님.
- 예를 들어, 검정에서 흰색으로 급격히 바뀌는 지점에서는 변화율이 크므로 양수가 됨.
- ramp을 따라 밝기가 변하는 과정에서도 0이 아님.
- 점진적으로 밝기가 변하는 부분에서는 변화율이 어느정도 일정하겠지만 0은 아님.
- 즉, 부드러운 그라데이션에서는 미분값이 일정한 값을 가짐.
이계도함수의 특징
- 일정한 밝기를 가진 영역에서는 0임.
- 변화가 없으면 도함수도 일정하니까 그 차이인 이계도함수도 0.
- step가 시작되는 지점에서는 0이 아님.
- 도함수가 크게 바뀌는 걸 따라서 이계도함수도 당연히 같이 바뀜.
- 그 부분에선 갑자기 확 크거나 작은 값을 가지게 됨.
- 상수 기울기를 가진 ramp에서는 0임.
- 도함수가 0이 아니어도, 도함수의 차이가 0이 되니까 이계도함수도 0.
zero crossing
- 이계도함수가 x축을 가로질러서(cross) 부호(sign)가 변하는 지점.
이계도함수를 구하는 이유??
- 실제 현실의 이미지들에선 카메라로 정확히 초점 맞춰 찍는 게 아니기에,
- 엣지 부분이 흐릿흐릿하게 찍히는 경우가 많음. 아님 박스 필터같은 걸 씌워서 흐릿해졌듯.
- 즉, step이 잘 안나타나고, ramp가 더 자주 나타남.
- 근데 그림에 나와있듯이 ramp는 zero crossing이 뚜렷하게 나타나진 않고, step에서 zero crossing이 뚜렷하게 나타남.
- 즉, 이계도함수는 step을 더 민감하게 찾아줄 수 있음.
- 따라서 step을 찾기 용이하다!
- 아마 도함수로 step찾는 것보다 이게 더 유리해서 그런듯. =0을 구하면 되니까.
The Laplacian

- 우린 이제 x축이 아닌 y축도 있음.
- 라플라시안(Laplacian):
- 미분 연산 중 하나로, 주어진 함수의 이계도함수의 합임.
- 각 축으로 두 번씩 미분한 걸 더한 것.
- 위는 2차원에서의 라플라시안 연산 수식임.
- 우리는 이를 2차 미분의 zero crossing으로 엣지를 검출할 때 사용할 거임.
- 변화량을 나타내는 기호 델타를 뒤집어놓은 모양인데. 저건 델이라고 읽음 기호.
- 제곱을 쓴 건 두 번 미분했다는 거.
- x, y를 더한 건, 공간 자체가 1차원이 아니라는 거임.
- 쉽게 말하면 예시에선 각각의 축에 대하여 각각 두 번씩 미분하고 더한 것.
- 계산 결과는, 자기 주변 것들 더해서 그 개수만큼 자기꺼 값 뺀 것임.
- 또는 각 방향에 대한 변화량의 합이라고 볼 수도 있음.
- 방향에 독립적(Isotropic)임.
- 특정 방향에 관계없이 동일한 방식으로 작동한다는 거.
- rotation invariant(회전 불변)하다고도 부름.

- 왼쪽은 4-이웃, 오른쪽은 8-이웃을 사용한 라플라시안 연산의 계수를 나타낸 것.
- x변화량과 y변화량을 더한 것.
라플라시안의 특징
- 강한 밝기 변화가 있는 부분(즉, step)을 강조함.
- 밝기가 천천히 변하는 영역(즉, ramp)은 강조하지 않고, 오히려 그 부분을 약하게 만듦.

- 왼쪽은 원본 이미지, 가운데는 이계도함수(라플라시안 연산 결과)를 구한 것임.
- 저건 당연히 0(검정) 값이 많은 게 당연함.
- 근데, 저 0 중에선 실제론 음수인데 0으로 나타난 것도 있을 거임.
- ex. 갑자기 밝아지면 한 순간 양수가 나올건데, 그러다 갑자기 밝아지는 게 끝나면 한 순간 음수가 나올 거임.
- 이를 보기 위해 중간값정도의 상수(ex. 128)을 더해 줌.
- 그 결과, 오른쪽처럼 회색빛이 나오는 부분이 가운데의 검정임을 알 수 있음.
- 그러면 저 왼쪽 아래 부분에서, 엣지 부분에 step이 나타나는 걸 볼 수 있음.
- 갑자기 큰 양수가 나왔다가, 갑자기 작은 음수가 step에 나오고 있음.
- 그러면, 저 step 부분을 밝은 데를 더 많게, 어두운 곳을 더 어둡게 해주면 더 엣지가 선명하게 되겠구나!!
- 그걸 라플라시안 값을 가지고 처리하면 되겠는데??
Image Sharpening with Laplacian

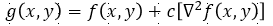
- 원본 이미지다가, 라플라시안에 음수 c를 곱한 값을 더한 거임.
- 가운데는 그냥 더한 거(c 적당한 값), 오른쪽은 c의 절댓값을 더 크게 해서 더한 것.
- 여기서 c는 음수로 절댓값 말하는 거. 즉, 실제론 빼준 거라고 볼 수 있지.
- 그 결과, 엣지가 선명해진 걸 볼 수 있음.
- 저런 엣지를 선명하게 하는 연산을 사프닝이라고 정의함.
참고) 저 라플라시안을 빼주는 게 어떻게 엣지를 강조(샤프닝)하는 거냐??
- 위처럼 어두웠다가 갑자기 밝아지는 step에서는, 라플라시안은 반대로 급격히 커졌다가 급격히 작아지잖음??
- 그러면 어두운(작은) 값에서 큰 값을 빼 주면 당연히 더 어두워지고, 그 반대도 마찬가지지.
- 그래서 라플라시안 값을 빼 주는 게 엣지 강조(샤프닝)이 되는 거임.
Unsharp Masking and Highboost Filtering



- 우리가 가우시안으로 첫 번째 이미지를 두 번째처럼 블러한다고 생각해 보자.
- 그러면 원본에서 블러한 이미지를 빼면, 저 세 번째 결과 그래프가 나올 거임.
- 얘를 원본에다 더해주면, 네 번째 결과 그래프가 나옴.
- 밝아지려고 할 때 한번 어두워졌다 밝아지고, 다시 그만 밝아지려고 할 때 한번 밝아졌다가 돌아옴.
- 즉, 얘도 샤프닝(엣지 강조하기)다!! unsharp라고 되어있지만 얘도 샤프닝임.
- 여기서 세 번째 그래프를 g_mask라고 부르는데,
- 얘는 이미지의 블러한 변화율만 기록하고 있음.
- 얘를 더해주면 엣지가 더 선명해진다.
- 그래프 순서대로 f, f_bar, g_mask, g.

- 순서대로 원본, blur, g_mask(변화율), Unsharp masking 결과, Highboost filtering 결과.
- k = 1일때:
- Unsharp masking이라 부름.
- 엣지가 적당히 강조가 됨.
- k > 1일때:
- Highboost filtering이라 부름.
- 엣지가 더 강조가 많이 됨.
- k < 1일때:
- Unsharp masking하는 게 덜 강조되겠지(엣지가 선명해지긴 하겠다만)
- k < 0이면 blur랑 비슷한 동작을 하게 됨.
Gradient

- x축 미분, y축 미분한 건 성질이 달라서 합하기가 어려움.
- 그래서 벡터로 나타내겠고, 그런 벡터를 gradient라고 부르겠다.
- 얘는 앞에 제곱이 없으니까 그냥 한 번만 미분한 건데, 그냥 미분기호를 쓴 게 아니니까, 아까랑 똑같이 차원이 1이 아니라는 거임.
- 각 방향으로 한 번씩 미분한 값들을 벡터로 나타낸 것임.

- 벡터는 크기와 방향으로 이루어져 있잖음??
- gradient의 크기(Magnitude)를 위처럼 구할 수 있음.
- non-linear한다는 거 알고 가자.
- 이 값이 클 수록 엣지 강도가 강하다(밝기가 step하게 변할 확률이 높다)는 걸 의미함.
- gradient의 방향은 나 (x, y)를 기준으로, 어느 방향으로 밝아지고 있냐를 의미함.
- 그 쪽 방향으로 밝기가 밝아지고 있다는 거.
gradient 계산 예시(GPT)
이제 정확하게 설명을 해드릴게요. 주어진 이미지를 사용해서 그래디언트가 어떻게 계산되는지 살펴보겠습니다.
입력 이미지:
[ 0 0 0 0 255 ]
[ 0 0 0 0 255 ]
[ 0 0 0 0 255 ]
[ 0 0 0 0 255 ]
[ 0 0 0 0 255 ]
이 이미지는 수평 방향에서만 변화가 있고, 수직 방향에서는 변화가 없습니다. 각 행의 마지막 열(5번째 열)만 255이고 나머지는 0입니다. 즉, 이 이미지는 수평 방향으로만 밝기 변화가 있는 이미지입니다.
그래디언트 계산
이미지의 각 픽셀에 대해 그래디언트를 계산할 때, 우리는 주로 미분을 사용합니다. 그 중에서도 차분(difference) 방식으로 근사할 수 있습니다.
수평 그래디언트 (dx)
수평 그래디언트는 좌우 변화량을 나타내며, 수식으로는 다음과 같이 표현할 수 있습니다:
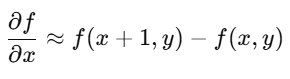
즉, 각 픽셀에서 오른쪽 픽셀과의 차이를 계산합니다.
- 첫 번째 행:
- 두 번째 행부터 다섯 번째 행까지도 동일한 방식으로 계산됩니다:
따라서 수평 그래디언트는 마지막 열에서 255이고 나머지 부분에서는 0이 됩니다.
수직 그래디언트 (dy)
수직 그래디언트는 위아래 변화량을 나타내며, 수식으로는 다음과 같이 표현할 수 있습니다:
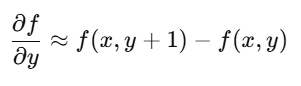
즉, 각 픽셀에서 아래쪽 픽셀과의 차이를 계산합니다.
- 첫 번째 열부터 다섯 번째 열까지 (y 방향)에서는 수직 방향 변화가 없습니다. 왜냐하면, 첫 번째 열부터 다섯 번째 열까지 모두 0이고, 아래쪽 행에서도 동일하게 0이기 때문입니다.
따라서 수직 그래디언트는 모두 0입니다.
Gradient & Sobel Operator

- Basic gradient
- $g_y=z_8-z_5, g_x=z_6-z_5$
- 중앙 대칭적이지 않음. 왜 다음거만 보냐? 이전 꺼는 고려 안하고? 불편…
- Symmetric gradient
- $g_y=z_8-z_2, g_x=z_6-z_4$
- 대칭적으로는 이런 수식이 가능
- 엄밀하게는 저거 2로 나눠야 하지만, 우리는 방향만 보고 싶으니까 굳이 나누진 않음.
- 3x3의 경우:
- $𝑔_𝑦=𝜕𝑓/𝜕𝑦=(𝑧_7+2𝑧_8+𝑧_9 )−(𝑧_1+2𝑧_2+𝑧_3 )$
- $𝑔_𝑥=𝜕𝑓/𝜕𝑥=(𝑧_3+2𝑧_6+𝑧_9 )−(𝑧_1+2𝑧_4+𝑧_7 )$
- 저런 식으로 각 미분값(=그래디언트의 요소들)을 정의한 것을 ‘소벨 연산자(Sobel Operator)’라고 부름. 또는 소벨 필터.
- x축을 미분할 때, 저 z6 - z4를 할 때, 저 z6이 이상한 놈이면 어케?? 노이즈면?? 그래서 z9, z3을 z6에 섞어보자. 근데 비율을 좀 가우시안 때 했던 것처럼 조정해서. 그러면 z6이 노이즈가 껴 있어도, z9랑 z3이 그걸 좀 덜 노이즈스럽게 만들어줌.
- 그래서 비율을 저렇게 한 거임. 가운데 것만 2배 하자.
- 그러면 노이즈로부터 조금 더 안쉽된다고 함.
- 대충 가우시안 블러 때 했던 그거랑 비슷한 느낌.
- 즉 두 개의 3x3 커널을 사용한 거임.
Sobel Operator

- 왼쪽이 원본, 오른쪽은 x축과 y축 각각에 대해 미분해 구한 gradient의 magnitude 값을 그려준 거임.
- magnitude는 항상 0 또는 양수고, 색이 변하는 곳에서만 0이 아닌 값을 가짐.
- 또한 색이 급격하게 변하는 곳(즉 step)에서 magnitude는 급격하게 큰 값을 가짐.
- 따라서, magnitude가 급격하게 커진 곳이 edge구나! 하고 알아낼 수 있음.
- 물론 얘는 라플라시안과 달리, step이 아닌 ramp들 또한 어느정도 적당한 밝기로 알아낼 수 있음.
- 또 뭐 ramp가 아니어도 그냥 객체 내부 색 변화도 보이겠지 당연히.
Combining Spatial Enhancement

- 지금까지 배운 것들을 종합하면, 다음과 같이 다양한 것들을 알아볼 수 있음.
- (a)는 원본.
- 거기에 라플라시안을 씌우니까 엣지가 보이기 시작한 게 (b). 상수 더해서 검정을 회색으로 나타내줌.
- 그래서 원본에 라플라시안을 합쳐서, 원본에서 라플라시안을 빼 보면 (c)는 저렇게 샤프닝(엣지가 강조)된 그림이 됨.
- 이제 이미지에 소벨 연산자를 사용해 magnitude를 구해 그리면 (d)가 나옴.

- 그리고 그렇게 구한 magnitude를 어찌저찌 잘 해가지고,
- 마지막에 감마 보정까지 해주면??
- 최종 결과 (g)가 나옴.
- 교수님 여담) 여기서 대부분의 이미지 보정의 효과는 감마 보정이 해줌.
- 감마 보정이 대비를 올려주는 그 효과가 너무 좋아서 최소 절반 이상은 먹고 들어감.
'AI & Data > 컴퓨터 비전(CV)' 카테고리의 다른 글
| [영상처리] Ch3.1. Intensity Transformations (0) | 2025.04.07 |
|---|---|
| [영상처리] Ch2. Human Vision (0) | 2025.03.24 |
| [영상처리] Ch1. Introduction. (0) | 2025.03.10 |


